THE CENTRE CODES OF THE BUSH BARROW LOZENGE.
We have touched briefly upon codes occurring from the centre
fulcrum position of the Clandon Barrow Lozenge and will now probe the Bush
Barrow Lozenge to see if the same modus operandi was employed in its coding.
It will be remembered that the width of the Clandon Barrow inner diamond was
1.701 inches (lunar code), with a length of 2.3328 inches (dual coded as 2.33333
inches). The centre diamond of the Bush Barrow lozenge carries the exact same
width code (1.701 inches), but its length is reduced by 1.6 and achieves 1.458
inches (lunar code). This can also be interpreted as 1.45833333 inches for
overland distance use and both numbers are mnemonically representative of
the length of the ancient Greek Pygon measurement (14.58 inches), in either
lunar or overland distance guises.
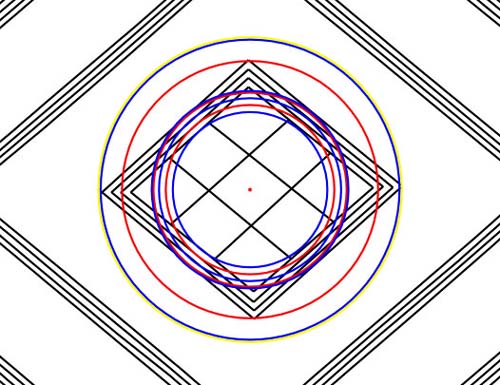
The circles expanding out from the centre of the Bush Barrow
Lozenge were set to very meaningful radius or diameter values, which are found
encoded into ancient structures from Egypt to New Zealand. Again, all circles
shown were precisely measured within AutoCAD, over a correctly scaled drawing
of the Bush Barrow Lozenge artefact. Here are the codes that the original
artisan placed into the centre section of the lozenge memory device:
- The width (top to bottom) of the diamond is 1.701 inches (red circle). There
are 1701 X 4 days in the 6804 day lunar nutation cycle (major standstill to
major standstill).
- The length (left to right) of the diamond is 1.458 inches (blue circle),
the radius of which falls precisely upon the station to the left, but marginally
short of the station to the right. This value is coding the latter era lunar
Pygon adopted by the Greeks.
- A second circle (yellow) has a diameter of 1.728 inches (radius .864) and
it falls precisely on the station to the right. This is one of the foremost
navigational values of antiquity.
The 4 pattern line positions (edges of the 3 raised, incised humps), in 4 quadrants,
comply to the following radii:
- There is positive coding for .56 inches and .55 inches radius respectively
(circle diameters of 1.12 & 1.1 inches respectively), with symbolic coding
for .54 inches (1.08 inches diameter). The value 56 was used copiously in
Sabbatical Calendar counts for the cycles of the Sun and Moon. The value 54
was very important for tracking the cycle of the Moon with mathematical ease.
- The value 55 was very important to navigation under an "11" series
of numbers and when a diameter, based upon 55 feet, is converted to a circumference
it achieves 172.8 feet ("6&8" series...easily divisible within
360-degrees of arc) This goes some way toward explaining why the 1.728 inch
code appears (left to right) in one of two centre diamond diameter codes.
This relationship between a diameter based upon 55 feet, converting to a 172.8
circumference (using a navigational rendition of PI @ 3.141818182) was, obviously,
much exploited in ancient chart plotting at sea. Alternatively, a diameter
based upon 56 feet ("7&8" series) converts to 176 feet ("11"
series...when using the PI rendition of 3.142857143 or 22/7). This is why
the British preserved the concept of 1760 yards in a mile...traceable back
to before King Athelstan (circa 939AD), who, in his day, used the ancient
"11" series measurements to create a "protective zone"
around his person called "The Kings Girth".
- .5184 inches radius (1.0368 inches diameter). This extremely important number
was multi-use and, obviously, featured prominently in navigational chart plotting,
where the straight line distance of 1 league (16500 feet) converts to a circumference
of 51840 feet (easily divisible by 360-degrees).
- .48 inches radius (.96 inches diameter). Again, a very important breakdown
value in 360-degrees or as a fluid mathematical progression.
- .44 inches radius (.88 inches diameter). An important "11" series
navigational number. There were 440 Egyptian Royal Cubits of 20.61818182 inches
each in the length of the Great Pyramid. (756 feet).
OTHER INCH RADIUS CODES AT THE 2ND, 3RD AND 4TH PATTERN POINTS (INNER DIAMOND).
The lozenge was a memory device, used for the recall of numerical values. It
seems that, like an accountant's ledger book, it should tally up between at
least 3 station points in each quadrant... those stations being:
- The overall distance from the centre to the most extreme outer pattern point.
- The overall distance from the most extreme pattern point back to the centre
of the owl's eye.
- The short distance from the centre of the lozenge to the centre of the owl's
eye.
Certainly, the distance of length, pattern point to pattern point across the
entire lozenge, seems to have been set at a recognisable, accumulative, coded
value. However, it's unlikely that this tremendously difficult to achieve design
feature had to apply to every consecutive coded distance amongst the inner diamonds,
as the codes fall into quite different number families. An "11" series
number is unlikely to produce a significant ratio value, for example, when added
to a "6&7" series number, etc. It seems more likely that circle
geometry coded values were achieved from the "owl eyes" stations,
then subtlety adjusted to give the most precise possible mnemonic readings from
other stations. The reader of the lozenge would visually detect, for example,
that a station sat at .79 of an inch from a fulcrum station and would immediately
think of 7920 leagues...the equatorial circumference of the Earth under the
"11" series system. A station hovering around 1.57 would mean 1.575
and 1.5708 simultaneously, the full numbers having been learned by rote and
repetition from "Masters of the Craft".
LEFT SIDE OF THE LOZENGE.
- The overall distance from the centre of the lozenge to the outer pattern
point was 3.6 inches. This was coding 360-degrees of arc. The return distance
from the outer pattern point to the centre of the owl's eye was 2.916 inches.
This value is 1/2 of 5.832 inches, which was related to the Roman "lunar"
Pace @ 58.32 inches or the Greek lunar Pygon @ 14.58 inches (5 X 2.916 inches
= 14.58 inches). The overall length of the Bush Barrow Lozenge was meant to
be 7.29 inches, which is 2.916 X 2.5 inches (1/2 a Greek Pygon or 1/8th of
a Roman Pace). The difference, therefore, between the overall distance to
the outer pattern point and the distance back to the centre of the owl's eye
is .684 inches. Half this value is 3.42. At Stonehenge one of the Station
Stones was carefully placed at 342-degrees azimuth from site centre. 180-degrees
opposed to that position was another Station Stone at 162-degrees azimuth.
The mnemonic use of this value appears to be related to setting out a 360-degree
circle into 20 positions with a spread of 18-degrees of arc, or 40 positions
with a spread of 9 degrees of arc. The two remaining stations on the lozenge
that haven't been mentioned, appear to be coded at .792 ("11" series
navigation) and .729 or .729166666 (lunar or overland) inches respectively.
THE RIGHT SIDE OF THE LOZENGE.
- There are two sets of coded values to consider on this side of the lozenge.
One set relates directly to the length of the Menkaure Pyramid of the Giza
Plateau and the other relates to half the base length of the Khafre Pyramid
of the Giza Plateau. The most extreme pattern point marking complies to a
position of 3.564 inches from the centre of the lozenge. Menkaure Pyramid
was 356.4 feet long.
- The "close proximity" overall distance from
the centre of the lozenge to a marked intersection near the most extreme pattern
point was coded to be 3.54375 inches. This is in homage to the lunar year
@ 354.375 days. The return distance from the outer pattern point to the eye
of the owl was 2.835 inches. The Khafre Pyramid (Egypt's pyramid of the Moon)
had a base perimeter length of 2835 feet, or 4 sides @ 708.75 feet each (15/16ths
the length of the Great Pyramid @ 756 feet). Half of 708.75 is 354.375 (the
number of days in a lunar year). The difference, therefore, between the overall
distance and the distance back to the owl's eye is .70875 inches (the distance
from the centre of the lozenge to the owl's eye station)...2.835 + .70875
= 3.54375. The two remaining pattern points by the owl's eye that haven't
been mentioned, appear to be .81 (rounded PHI & true PHI) and .756 inches,
respectively.
THE OVERALL LENGTH OF THE LOZENGE, OUTER TIP TO OUTER
TIP.
Although measurements supplied by Mr. Paul Robinson of
the Devizes Museum are only correct to the last millimetre (+ or -), it can
be safely assumed that the astronomer/ artisan who fabricated the lozenge intended
that it achieve a length of 7.29 inches. From the centre of the lozenge to the
left end point should have achieved 3.6525 inches. This was in homage to the
solar year @ 365.25 days. The length, therefore, requires that the distance
from the outmost pattern point to the end exterior point be .0525 inches. This
very important increment was the basis of many ancient measurement systems and,
on the inner rim of the Sarsen Circle lintels at Stonehenge, 5.25 inches represented
1/2 a degree of arc.
The length to the right from the centre of the lozenge
could be read in two main ways. It was either 3.564 inches + .081 inches or
3.54375 inches + .09375 inches. The 9375 mathematical progression was very important
to compass and lunar determinations or navigation under the "11" series
of numbers.
The entire diameter, in inches, is read as a string of
accumulative codes in any of the following, perfect combinations of significant
ancient numbers and useful ratio values:
- .0525 + 2.916 + .684 + .70875 + 2.835 + .09375 =
7.29 inches (1/2 a Greek Pygon), or:
- .0525 + 3.6 + 3.54375 +.09375 = 7.29 inches, or:
- .0525 + 3.6 + 3.564 + .0735 = 7.29 inches, or:
- 3.6 + 3.564 + 1.26 = 7.29 inches or:
- 7.29 ÷ 2 = 3.645 - 3.54375 =
.10125 or
- 7.29 ÷ 2 = 3.645 - 3.6 = .045,
or:
- .0525 + 3.6 = 3.6525 (solar year = 365.25 days)...left side total, or:
- .070875 + 2.835 = 3.54375...length extending to a significant pattern point...(lunar
year = 354.375 days).
There is some clever sharing, juggling or substitution
of coded values to the left & right or overall, which introduces many very
important mathematical progression values, like .10125 (lunar, navigation).
The fact that every number in the above list was essential to ancient lunar,
solar or navigational functions suggests strongly that this was the ancient,
combined set of numbers built into the length of the Bush Barrow lozenge.
THE TOP OF THE LOZENGE TO THE BOTTOM.
It seems obligatory that the width of the Bush Barrow
Lozenge and the length of the Clandon Barrow Lozenge were meant to be 6.18034
inches, outer edge to outer edge. The true dimension, in each case, might have
been set to what was visually achievable at around 6.18 inches. This value (based
upon PHI...10 inches ÷ 1.6180339) was the foundation formula for
the fabrication of all "official" ancient circular volume vessels
used by the cousin nations of the Mediterranean and, by association, Europe.
By use of this value, all "official standard" vessels, cups or tubs
would equate to exact cubic measures. Those exact and precise volumes could
then be transferred (poured) into other robust, sturdy, conveniently shaped
and sized "amphora" jars, used for trading liquid or dry measure goods
around the Mediterranean Basin, or overland across Continental Europe and Africa.
The Bush Barrow and Clandon Barrow lozenges, conceivably, were used for checking
the integrity of "bushel" volume tubs in the ancient Wessex marketplaces
to ensure that merchants were dispensing correct measures to their customers.
A correct bushel tub would accommodate exactly 3 widths of the Bush Barrow Lozenge
or 3 lengths of the Clandon Barrow Lozenge across its circular base.
THE REMAINING 3 CODES AT THE TOP OF THE INNER DIAMOND.
- .6804 (lunar nutation), .63 ("6&7" series navigation, etc.),
.5832 (lunar).
THE REMAINING CODES AT THE BOTTOM OF THE INNER DIAMOND.
- .6875 ("11" series navigation), .64 ("8" series, compass),
.594 (Menkaure Pyramid, navigation).
Beyond the foregoing diameters listed for circles within this section, individual
values can be multiplied or divided by companion values to create square inch
areas or ratios for use in astronomical or navigational determinations
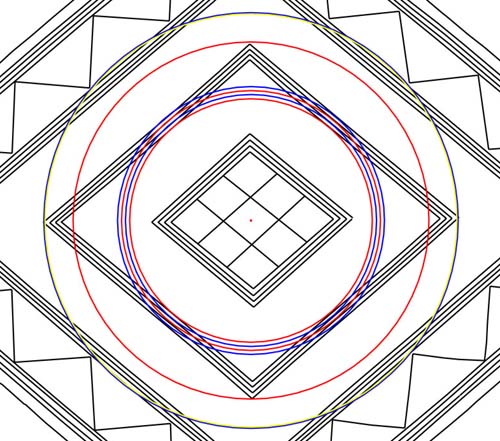 .
.
The diameter width (red circle) of the 2nd diamond is 3.024
inches. This width is in homage to the perimeter value of the Great Pyramid
(3024 feet...1/2 a minute of Earth equatorial circumference arc under the pyramid's
"6&7" geodetic system....or 3025 feet...1/2 a minute of arc under
the "11" series system). The length of the diamond (blue circle)
is 3.52 inches (1.76 radius). This is accentuating the "11" series
navigational system, incorporating the league (16500 feet), mile (5280 feet),
furlong (660 feet), chain (66 feet), rod/ perch (16.5 feet), fathom (5.5 feet)
and link (7.92 inches). The yellow circle, sitting adjacent to the outer
blue circle, is 3.5 inches wide (1.75 radius). This code would also have been
included, as it provides an important conversion ratio for elevating 7th segments
of a 360 degree circle into whole number values in a 630-degree circle. Therefore,
51.42857143 -degrees X 1.75 = 90.
The 4 pattern line positions (edges of the 3 raised, incised humps), in 4 quadrants,
comply to the following radii:
- The outermost pattern line is touched by a circle (blue) of 1.134 inches.
The circle has a diameter, therefore, of 2.268 inches. The Great Pyramid is
756 feet per side and a total of 3 sides equates to 2268 feet. This is a very
important lunar code and 3 X 2268 = 6804...the duration in days of the lunar
nutation cycle. The width of the Station Stones rectangle at Stonehenge is
113.4 feet and carries the nutation cycle code also.
- The second pattern line is touched by a circle of 1.1 inches radius or 2.2
diameter. This is "11" series coding. The circular design width
of the Sarsen Circle at Stonehenge was 110 feet, although it was made slightly
elliptical to achieve 113.4 feet from 225-degrees azimuth to 45-degrees azimuth.
- The third pattern line is touched by a circle of 1.066666 inches radius
or 2.1333333 inches diameter. This was a simple conversion ratio for 15/16ths.
The Great Pyramid's length @ 756 feet ÷
1.0666666 = 708.75 feet (the length of the Khafre Pyramid).
- The fourth pattern line is touched by a circle of 1.03090909 inches or 2.061818182
inches diameter. This circle is of extreme importance and means upwards of
6 things simultaneously. This circle is in homage to the equatorial circumference
of the Earth and the 6 major types of Egyptian Royal Cubits that carried the
equatorial circumference formula in their lengths. This is what they did:
SYSTEM 1. AN EQUATORIAL CIRCUMFERENCE OF 25000 MILES.
The rod for this system would be 20.833333 inches X 1200 =
25000 (read as miles).
The 25000-mile circumference concept was, probably, only ever
a convenient way of describing the approximate circumference of the Earth. Under
this calibration the Earth would be 132000000 feet in equatorial circumference,
which is an excess on the modern, accepted circumference (24902-miles) by 98-miles.
SYSTEM 2: AN EQUATORIAL CIRCUMFERENCE OF 24883.2-MILES.
The rod for this system would be 20.736 inches X 1200 = 24883.2
(read as miles).
This is, plausibly, the ancient "true" size of the equatorial
circumference (12 X 12 X 12 X 12 X 1.2-miles). One second of arc for this circumference
would be 101.376 feet, and that's the width of the stybolite platform upon which
the Parthenon of Athens sits. Ancient surveying markers, still intact in the
Waitapu Valley of Northern New Zealand, sit 12441.6 feet distant from each other
(12441.6 X 2 = 24883.2). These were anciently erected by New Zealand's now extinct
"Stonebuilder" population.
SYSTEM 3: AN EQUATORIAL CIRCUMFERENCE OF 24857.95455-MILES.
The rod for this system would be 20.71496212 inches X 1200
= 24857.95455 (read as miles).
This is a shared Egyptian, Greek and Roman system that works in
progressions of the number "7". It seems to be founded upon 5000 Egyptian
Atur of 26250 feet each (5 Greek miles). One of the concepts of ancient metrology,
which survived into mediaeval times, was that 75 Roman miles represented 1-degree
of arc for the world, although scholars of the time had, seemingly, no lingering
knowledge of the actual, former length of a Roman foot...until professor of
geometry, John Greaves did a careful reassessment, in Rome, in 1639AD.
If we multiply a foot of 11.66666 inches X 5000 we get a Roman
mile of 58333.3333-inches (or 1000 Roman Paces). If 75 such Roman miles represent
1-degree of arc for the world, then that equates to 4375000-inches or 364583.33333
British feet of 12-inches each. This value, multiplied by 360 = 131250000 British
feet or 135000000 Roman feet. These lengths are also 12500000 Hebrew Reeds of
10.5 feet each or 125000000 Greek feet of 12.6-inches each. Essentially, this
very plausible coded representation for the size of the Earth is a purely "7"
series way of calibrating the equatorial circumference. The sum of 131250000
feet equals 24857.955455 British miles, 27000 Roman miles or 25000 Greek miles.
This same circumference was probably 5000 Egyptian Atur of 26250 British feet
each. The 131250000 British feet calibration does not work at all well according
to the 5280 feet mile, which is an "11" series numerical progression.
It does, however, break down very well into degrees, minutes and seconds of
arc under the Egyptian, Assyrian, Greek, Hebrew or Roman "7" series
measurement increments.
SYSTEM 4: AN EQUATORIAL CIRCUMFERENCE OF 24750-MILES.
The rod for this system would be 20.625 inches X 1200 = 24750
(read as miles).
This was, undoubtedly, a much used system and the most popular
for "straight line" sailing, as it's founded upon an "11"
series of numbers and became the basis of the ancient British league (16500
feet), mile (5280 feet), furlong (660 feet), chain (66 feet), rod/ perch (16.5
feet), fathom (formerly 5.5 feet) and link (7.92 inches) measurement system.
Under this early Egyptian system the Great Pyramid was considered to have a
base perimeter of 3025 feet (55 squared) instead of 3024 feet. This method of
reading the Great Pyramid required the symbolic elongation of each side by 3
inches, such that they would comply to "11" series numbers and 3025
feet was called 1/2 a minute of equatorial circumference arc for the Earth.
SYSTEM 5: AN EQUATORIAL CIRCUMFERENCE OF 24741.81818-MILES.
The rod for this system would be 20.61818182 inches X 1200
= 24741.81818 (read as miles).
This is the "literal" Great Pyramid system for calibrating
the size of the Earth in a combined "6 & 7" mathematical progression
reading (based upon the number 42). It appears to have been the most used system,
in consideration of the "6& 7" measuring capability built into
all known measurement standards of the ancient Mediterranean Basin. Although
the "7" based measurements disappeared from general use in Britain
during the latter Christian era, the "6" and "11" based
measurements remained. The ancient "7" based Mediterranean measurements
are found, however, to be strongly represented in the Bush Barrow and Clandon
Barrow lozenges, indicating that such measurements were alive and well in England
when the lozenges were fabricated.
Under the "6 & 7" system the Great Pyramid's perimeter
was read as 3024 feet and this represented 1/2 a minute of equatorial arc for
the Earth. The circumference of the Earth was read as 130636800 feet and this
broke down very fluidly into degrees (362880 feet...the literal perimeter measurement
of the Great Pyramid was 36288 inches), minutes (6048 feet...two circuits of
the Great Pyramid was 6084 feet) and seconds (100.8 feet... the inner diameter
of one section of the slightly elliptical Sarsen circle at Stonehenge is 100.8
feet). The 6, 7, and 11 systems were wonderful to navigate by, converting linear
distances covered into easily decipherable chart plotting circles that would
break down into degrees, minutes and seconds of arc. Under these systems, calculating
degree angles from point of departure to destination was simple to accomplish
and the relative position of the ship could always be known.
SYSTEM 6: AN EQUATORIAL CIRCUMFERENCE OF 24711.79047-MILES.
The rod for this system would be 20.59315873 inches X 1200
= 24711.79047 (read as miles).
The Great Pyramid was built in such a way that all of its dimensions
could be read (symbolically) according to PHI increments. The literal dimensions
of the Great Pyramid break down into increments of 1.62 inches and the PHI ratio
is 1.6180339 (rounding upward to 1.62). This duality of reading is found on
many European/ Mediterranean/ Indus Valley/ American/ Oceanic monuments of antiquity,
where the dimensions can be read in either rounded PHI or pure PHI increments.
This is certainly true of Stonehenge. The Great Pyramid's length could be read
as 280 rounded Megalithic Yards (of 32.4 inches...756 feet...literal length)
or 280 true Megalithic Yards of 32.360678 inches (755.0824867 feet...symbolic
PHI length). This would mean that 1/2 a minute of equatorial arc, under the
pyramid's pure PHI assignment, would be 3020.329947 feet.
The PHI ratio was difficult to work with, due to the complex numbers
it produced, nevertheless the ancient mathematicians found several methods to
"tame" PHI and one of these was to use (at least) "rounded PHI"
in all or most major building applications. Many statuettes or panels of antiquity
incorporated pure PHI dimensions. The majority of circles at Stonehenge (except
where carrying other types of coding...such as in the case of "Z"
Holes) are in a pure PHI relationship to each other, but reduce in whole number
diameters (466, 288, 178, 110 feet respectively, etc.) in a clever numerical
manipulation of PHI.
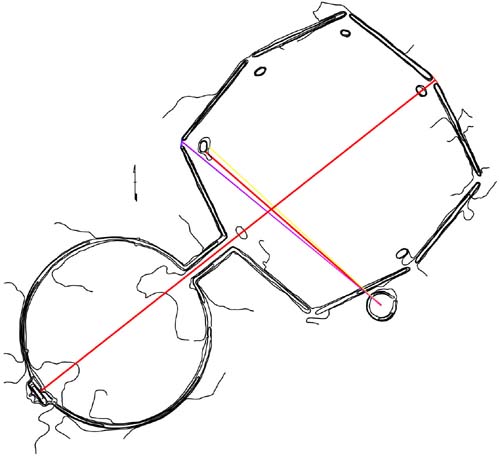
This is a picture of the huge Octagon of Newark Ohio, redrawn
exactly to scale in AutoCAD over an official survey map. The 1958 survey was
conducted by Abrams Aerial Survey Corporation of Lansing, Michigan for the City
of Newark, Ohio. The official survey charts were donated to this researcher
for "Octagon analysis" by researcher Patricia Mason of Newark, Ohio
http://greatserpentmound.org/articles/giants.html
. The coloured lines appearing on this above drawing show how the selfsame angle,
length and Earth equatorial values, encoded in micro-scale within the Clandon
Barrow and Bush Barrow lozenges, were encoded in macro-scale within the giant
Octagon, geometric earth embankment complex. Here's an explanation of what the
coloured lines mean:
- The red line, running up diagonally from the lower left to the upper right,
is on an azimuth angle of 51.84-degrees. This is exactly the same degree angle
as one arm of the central crosses of both the Clandon Barrow and Bush Barrow
lozenges.
- The red line, referred to, runs for exactly 2835 feet from a specially formed,
small alcove at the front of the altar, to the uttermost extremities of the
site. The line stops precisely at a central point of the gateway, in line
with the outer edge of the converging mounds to each side. The Khafre Pyramid
@ 708.75 feet per side has a perimeter value of 2835 feet. This distance,
in feet, would represent, in days, 8 lunar years of 354.375 days each.
- The overall length of the whole Octagon complex ( from the rear of the altar
to the extremity postion of the gate) was coded to be 2880 feet. The Aubrey
Circle at Stonehenge is 288 feet in diameter and this is one of the most dynamic
values of antiquity, occurring on many sites.
- Just as 2835 is a lunar code, so also is 1701 (the diamonds housing the
St. Andrew's Cross arms on both the Clandon Barrow and Bush Barrow lozenges
were encased within circles of 1.701 inches). The value 1701 is coding 1/4th
of the lunar nutation cycle of 6804-days.
- The red line running up to the left from a small circle complex, adjacent
to the Octagon, is on an azimuth angle of 311.04-degrees. This is exactly
the same degree angle as one arm of the central crosses of both the Clandon
Barrow and Bush Barrow lozenges.
- The red line just mentioned runs for 1313.83296 feet (AutoCAD generated),
brushing the edge of a specially built earth peninsula, to touch the nose
position of the 2nd tier of the small mound. Although the present, dilapidated
state of the small mound, after, possibly, thousands of years of neglect and
erosion, might show 2 feet of error in the reading, the intended distance
code was, originally, 100000th of the "true" equatorial circumference
of the Earth @ 24883.2 miles (12 X 12 X 12 X 12 X 1.2 miles) or 131383296
feet.
- The azimuth angle of this red line is 311.04-degrees. With the world equatorial
circumference set at 24883.2-miles, a 1/8th segment would be 3110.4-miles.
- From the centre of the circle embankment component of the Octagon to the
centre of the octagonal component, the distance is 1555.2 feet. This is half
of 3110.4 feet and, if feet were substituted for miles, 1555.2 miles would
represent a 1/16th segment of the "true" equatorial circumference
of the Earth.
THE EQUATORIAL CODES FALLING ONTO THE SMALL MOUND PENINSULA AT THE OCTAGON.
- The largest value encountered in sites or artefacts, describing the equatorial
circumference of the Earth, is 25000 miles or 132000000 feet. As stated, this
seems to be based upon an Egyptian Royal Cubit of 20.8333333 inches length.
Under such a system, 1/8th of the circumference would be 3125 miles. In accordance
with the system used to code the 24883.2-mile system, a line (yellow) is sent
out for 1320 feet at an azimuth angle of 312.5-degrees. The line touches the
base tier of the small mound. This position was, undoubtedly, once marked
by a stone at the Octagon. It's interesting to note that "Z" Holes,
at Stonehenge, is 132 feet in diameter and that an ancient league (16500 feet)
was 3.125 miles.
- A Roman calibration for the equatorial circumference was 131250000 feet
(27000 Roman Miles, 25000 Greek Miles, 24857.95455 British miles or 5000 Egyptian
Atur). A line (green) is sent out for 1312.5 feet at an azimuth angle of 310.724-degrees.
It nicely dissects the earth peninsula appendage, which seems to have been
built specifically to accommodate the 24883.2-mile coding brushing to the
peninsula side.
THE GATEWAY CODES AT THE OCTAGON.
The primary purpose of the small mound was related to special codes running
between the other small inner mounds and this geodetic coding seems to have
been a secondary function. The more generally used Earth equatorial circumference
codes, lending themselves very fluidly to world navigation, were separated out
and placed into the gateway. These were accompanied by the PHI equatorial coding
system, which was probably only ever used in certain scientific calculations
to do with PHI harmonics in nature (the way nature works). Let's look at these
other systems, situated over in the gateway.
- The "11" series was a marvelous mathematical system that worked
in conjunction with the "6&7" system. If the "11"
system was to be used for straight line sailing, then the circumference generated
by it would be "6" based (and perfectly divisible by 360-degrees).
The "11" system described the Earth as 7920 leagues or 24750 miles.
It appears to be coded as 1452 feet at the Octagon (.088 leagues, .275 miles,
2.2 furlongs, 22 chains, 88 rods/ perches, 264 fathoms or 2200 links). A 1/8th
segment of 24750 feet is 3093.75 miles and the coded position would have sat
at 309.375-degrees azimuth accordingly. This limit falls to the centre nose
line of the gateway mounds to each side, with the line terminating right of
centre.
- The "6&7" geodetic coding extends to the outer line of the
gateway mounds at 1458 feet (1200 Greek lunar Pygons of 14.58 inches each
or 300 Roman Paces of 58.32 inches each. This length was also 900 "rounded"
PHI feet (1.62 feet) or 10800 "rounded" PHI inches. The 1458 feet
distance would be 1/89600ths of the equatorial circumference under the Great
Pyramid "6&7" assignment. It can also be represented as 1458.333333
feet, which would have been more common in overland measurements, as its companion
measurement 1458 was for lunar coding. The line sits just right of centre
in the gateway.
- The "6&7" system doubles as a "rounded" PHI system,
as shown, but there was a "pure" PHI system as well, probably used
in assessing growth attributes of plants and harmonic aspects within nature
(further research might tell us more about how advanced those concepts were
within the ancient sciences). Under this assignment, the Earth would have
been viewed as having an equatorial circumference of 24711.79048 miles. A
1/8th segment of the Earth, under this calibration. would be 3088.9738 miles.
Our coded line, therefore goes out on an azimuth angle of 308.89738-degrees.
Whereas the 1458 feet measurement was 10800 "rounded" PHI inches,
this one will be 10800 "true" PHI inches of 1.6180339 inches each,
or 1456.2305 feet. This line extends slightly to the exterior of the gateway
embankments and just left of centre. It also, plausibly, would once have been
marked with a stone.
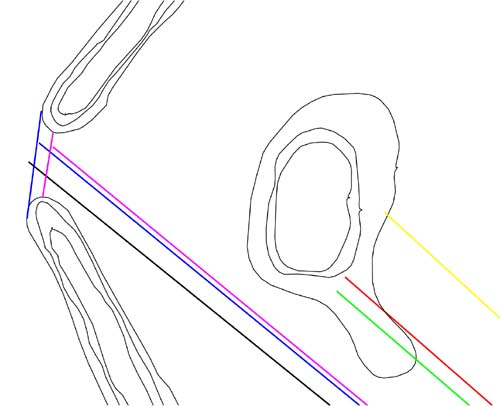
Lines within the Octagon, originating at the centre of a very important,
small embankment circle situated exterior to the Octagon. The black line represents
the PHI coding of the equatorial circumference. The blue line represents the
Great Pyramid's "6&7" equatorial assignment. The magenta line
represents the "11" series equatorial assignment. The Green line represents
the "Roman" "7" series equatorial assignment. The red line
represents the "true" equatorial assignment. The yellow line represents
the largest assignment of 25000 miles.
THE DIAMOND POINTS ON THE BUSH BARROW LOZENGE... TO THE LEFT.
- Radius measurements to the 3 stations not mentioned are 1.71 (compass),
1.666666 (3,4,5 triangle) and 1.6180339 (PHI) inches respectively.
THE DIAMOND POINTS TOP.
- Radius measurements to the 3 stations not mentioned are 1.458 (lunar), 1.4
(calendar, navigation), 1.3608 (lunar nutation) inches respectively.
THE DIAMOND POINTS TO THE RIGHT.
- Radius measurements to the 3 stations not mentioned are 1.71 (compass),
1.666666 (3,4,5 triangle) and 1.6180339 (PHI) inches respectively.
THE DIAMOND POINTS BOTTOM.
- Radius measurements to the 3 stations not mentioned are 1.458 (lunar), 1.4
(calendar, navigation), 1.3608 (lunar nutation) inches respectively.
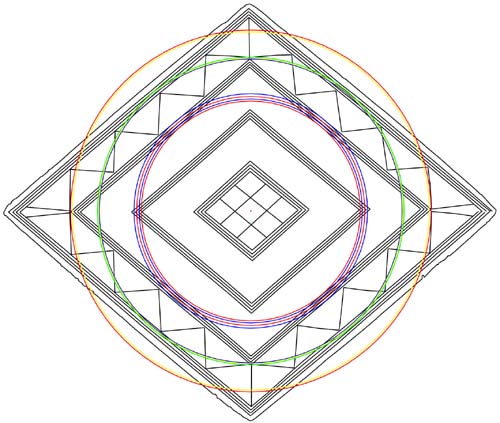
Moving outward to the next diamond, which gives 3 closely associated
codes in the width of the diamond top to bottom (combined circles blue, yellow,
green). The code to the top of the diamond is 2.24 inches radius. This value
provides a mathematical progression that applies to navigation under the Great
Pyramid "6&7" Earth equatorial circumference assignment. A progression
incorporating 2240 was adopted by King Henry VII after 1527 AD for the new English
ton and associated weights, which had also been used earlier in Egypt. The ancient
Egyptians used a "Sep" of 7000 grains, the same as King Henry VII's
pound.
The 4 outer points of the diamond swing close to the zigzagging
"V" chevrons and stations on the points of the chevrons provide 2
further dynamic codes. One of these is 2.25 inches, which was used copiously
in the 360-degree compass system. The sum of 22.5-degrees would be 1/8th of
a 360-degree circle.
Perhaps the most important value, positively coded into this
section, is a circle (green) with a radius of 2.268 inches (4.536 inches diameter).
The circle sweeps to the points of the chevron, top and bottom and has been
very carefully encoded. The Great Pyramid's flat altar floor was mathematically
calculated to sit at a vertical height of 453.6 feet. A rule of 3,4,5 triangles
was applied to achieve this height, wherein the pyramid's base length (756 feet)
was divided by 1.66666 to achieve 453.6 feet. In all 3,4,5 triangles one side
will always be 1.666666 less than the hypotenuse. It is in the pyramid's length
assignments, as opposed to it's vertical height assignments, that the codes
for the size of the Earth are found, as well as the formula for correctly fashioning
individual Egyptian Royal Cubits that comply to particular Earth size assignments
in different number families.
The radius length of the diamond is 2.66666 inches or 5.333333
inches in diameter (red circle). It will be remembered that the 1.0666666 ratio
(15/16ths conversion formula) was very important to ancient astronomers and
5.333333 is half of 10.6666666. This same width aspect of the diamond was also
read as 2.64 inches radius and 5.28 inches diameter (yellow circle), for coding
the "11" series overland distance system (5280 feet in a mile).
The 4 pattern line positions (edges of the 3 raised, incised humps),
in 4 quadrants, comply to the following radii:
- 1.728 inches radius (3.456 inches diameter). This is a tremendously important
navigational number. The diameter of Silbury Hill in Southern England was
intended to convey 550 feet to produce a circumference of 1728 feet (using
PI @ 3.141818182). The outer rim of the Sarsen Circle at Stonehenge was intended
to convey 345.6 feet, base upon a diameter of 110 feet. This relationship
between an "11" series diameter producing a "6" series
circumference (divisible by 360-degrees) would have been the basis of chart
plotting by navigators traversing the open seas in antiquity. We know ancient
European/ Mediterranean peoples got as far afield as New Zealand (the far
Isles of the Earth) thousands of years ago, as they left their code bearing
structures all over the landscape. It is from the ancient New Zealand structures
that this researcher has relearned the mathematical principles, whereby the
Bush Barrow and Clandon Barrow lozenges of the Northern Hemisphere can be
deciphered.
- Another diamond pattern line (bottom left) complies to a circle radius of
1.75 inches and closely complies to 1.76, which it would have also, mnemonically,
represented. The 1.75 ratio was used to elevate difficult 7th readings in
a 360-degree arena to easy to read whole numbers in a 630-degree arena. The
Brasen Sea calculator in the Temple of Solomon outer courtyard was a 630 degree
calculator, as was the Sarsen Circle inner rim at Stonehenge (circumference
315 feet or 630 feet ÷ 2). The
1.76 coding refers, of course, to "11" series navigation. A diameter
based upon a "7&8" number like 56 will produce an "11"
series circumference like 176 using the PI rendition of 22/7 (3.142857143).
- The second circle (red), falling upon the 2nd pattern line of the diamond
on 3 sides has a radius of 1.6875 inches or a diameter of 3.375 inches. A
progression based upon 1.6875 produces many useful lunar, calendar or compass
values.
- Another pattern line at the bottom left allows for a reading of 1.71 or
1.71875 inches respectively. These values produce reasonably useful progressions
related to 18 degree segments in a 360 degree circuit (1.71 progression) or
values used in "11" series navigation.
- The third pattern line (blue) is brushed by a circle of 1.65 inches radius
(3.3 inches diameter). This is, of course, related to "11" series
navigation and the rod/ perch was 16.5 feet or the ancient league 16500 feet...3.125
miles.
- Another pattern line at the bottom left complies to a circle radius of 1.68
feet or diameter of 3.36 inches. A mathematical progression based upon 1.68
will produce values that are very important to navigation under the Great
Pyramid "6&7" series assignment (based upon the number 42).
There was an early Israelite cubit of 1.68 inches. 3,4,5 triangles with an
adjacent of 126 feet, an opposite of 168 feet and a hypotenuse of 210 feet
were used at Stonehenge between the posts of the Aubrey Circle. The triangles,
which would have been formed by ropes brushing the posts, were for calculating
the azimuth angles of stars alighting onto the embankments. See: http://www.celticnz.co.nz/US16.html
- The fourth pattern line is brushed by a circle of 1.62 inches radius or
3.24 inches diameter. This is a rounded PHI increment and means 1.6180339
and 3.2360678 inches respectively as well. The measurement interval found
by Professor Alexander Thom on ancient, weatherworn British monument sites
and dubbed by him as the "Megalithic Yard" was, undoubtedly, (originally)
a PHI based increment of 32.360678 inches. Thom averaged it to 82.9 centimetres
(32.637795 inches).
THE OTHER PATTERN POINT CODES
The length of the 3rd outward diamond is, as stated, 5.33333 inches, for a
radius of 2.666666 inches. The other stations are:
- 2.625 inches radius (5.25 inches diameter). This is the base increment of
the reed (126 inches) much used in lunisolar calendar calculations. The latter
Greek measurement system was mostly based upon 525. Their mile was 5250 feet.
This position is dual coded and can also mean 2.618. This number provides
a mathematical progression leading to 31.416. PI is 3.1416.
- 2.57142857 inches radius (5.142857143 inches diameter). These values are
not as difficult as they look and are simply expressions of 7th segments of
360-degrees. For calendar work, especially, circles had to be divided up and
read in 7ths. The diameter in this case (5.142857143 inches) is expressing
1/70th of 360-degrees.
- 2.52 inches radius (5.04 inches diameter). The Great Pyramid @ 756 feet
is 3 X 252 feet. The Assyrian Royal Cubit was 25.2 inches and the Greek foot
used in most applications was half that value @ 12.6 inches. These values
were very useful in navigation and also for calculating lunar periods within
the lunar nutation cycle and the Sabbatical Calendar.
The width of the 3rd outward diamond is, as stated 4.48 inches, for a radius
of 2.24 inches. The other stations are:
- 2.2 inches radius (4.4 inches diameter). These increments refer, of course,
to "11" series navigation.
- 2.16 inches radius (4.32 inches diameter). The Great Pyramid @ 756 feet
was 432 Hebrew/ Celtic Royal Cubits of 21 inches each in length. In the Precession
of the Equinoxes (25920 years) the Sun spends 2160 years in each house of
the zodiac. The Moon is 2160 miles in diameter.
- 2.112 inches radius (4.224 inches diameter). These values are expressions
of the "11" series mile @ 5280 feet and 21120 feet would be 4 miles.
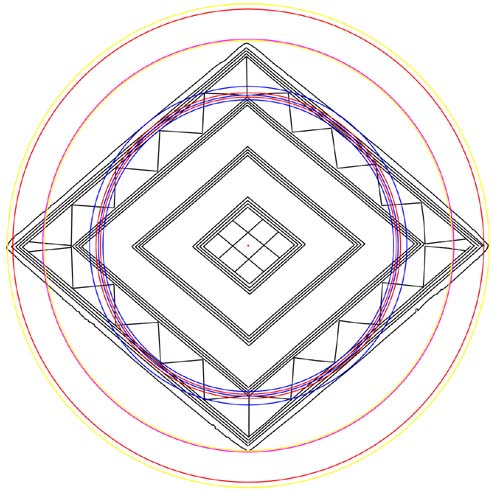
The final section of the Bush Barrow Lozenge. We have already
discussed the string of codes running through the length of the lozenge and
will now discuss the width codes, top to bottom. The overall distance (red circle)
was 6.1804 inches. The upper tip of the lozenge, especially, appears to be slightly
rounded and it would appear to have suffered some impact damage. If one follows
the natural edge lines on each side, they indicate that a slight elongation
of the lozenge is reasonable to bring it to a much improved point. Here's how
the code string runs from top to bottom.
- Overall distance = 6.1804 inches (PHI related code for correct fabrication
of volume vessels).
- Distance from the centre to the top outer edge, coded to be 3.07 inches
(used as 3.072"... navigation).
- Distance from the centre to the top pattern point = 2.9866666 inches (special
conversion ratio).
- Distance from the outer edge to the top pattern point = .08333333 inches
(3,4,5 triangle code).
- Distance from the top pattern point to the centre of the owl's eye = 2.4
inches (compass, calendar).
- Distance from the centre to the owl's eye = .586666666 inches ("11
series navigation).
- Distance from the centre to the bottom outer edge = 311.04 inches (true
equatorial circumference 1/8th code).
- Distance from the centre to the bottom pattern point = 3.024 inches (Great
Pyramid, 1/2 minute of arc).
- Distance from the bottom outer edge to the bottom pattern point = .0864
inches (solar, navigational).
- Distance from the bottom pattern point to the owl's eye = 2.43 inches (lunar
nutation cycle, Sabbatical Calendar).
- Distance from the centre to the bottom owl's eye = .594 inches (Menkaure
Pyramid, "11" series navigation).
CIRCLES TOUCHING THE OUTERMOST DIAMOND PATTERN LINES.
- 2.4 inches radius (4.8 inches diameter). This circle (blue) sweeps to the
outer edge of the lozenge.
- 2.304 inches radius (4.608 inches diameter). This circle sweeps to the outermost
pattern line. It carries a very important "11.52" code, much used
in antiquity. The Great Pyramid had a base length of 756 feet, a side diagonal
length of 576 feet and a flat top altar that was 44 feet square. Therefore,
the area of each face was 230400 square feet, or 8 Egyptian acres of 28800
square feet each. The Menkaure Pyramid, under its PHI assignment, was 11.52
Pyramid acres for all faces and the area occupied by the base.
- 2.268 inches radius (4.536 inches diameter). Three sides of the Great Pyramid
(756 feet per side) = 2268 feet (lunar code). The vertical height of the Great
Pyramid to the top of its altar floor was 453.6 feet (lunar and navigation).
- 2.24 inches radius (4.48 inches diameter). This value was used in navigation
under the Great Pyramid "6&7" assignment. It was also used for
lunar calculations.
- 2.2 inches radius (4.4 inches diameter). This value was used in "11"
series navigation.
THE PATTERN POINT CODES.
At the outermost pattern point sets, the artisan, engaged in marking the gold
sheet, added considerable extra coding. This was done by allowing a diagonal
line, coming from the left or right, to not meet at a common intersection. A
line coming up from the left, for example, might terminate at a slightly more
outlying position. It's obvious that the astronomer/ artisan was "packing
in" as many close proximity codes as possible. Here are the identifiable
codes residing in each quadrant:
LEFT POINTS @ 270-DEGREES.
- 3.6 inches radius (7.2 inches diameter). The position was dual coded to
also mean 3.571428571 inches. Again, this number isn't as difficult to conceive
of as it might first appear, and is simply a "7th" expression within
360-degrees. Under the ancient Earth equatorial circumference assignment a
distance of 100.8 feet was 1 second of arc. 360-degrees ÷
100.8 = 3.571428571-degrees. In a "7" series compass, based upon
630-degrees (like the inner rim of the Sarsen Circle at Stonehenge), this
position would be 6.25-degrees (3.571428571 X 1.75).
- 3.52 inches radius (7.04 inches diameter). This value relates to the "11"
series navigational system.
- 3.4722222 inches (6.944444). This relates to an Earth equatorial circumference
system based upon an Egyptian Royal Cubit of 20.833333 inches. Under this
system the Earth was considered to be 25000 miles in circumference. The position
was dual coded to also mean 3.456 inches (6.912 inches diameter). This relates
to the "true" equatorial circumference, which uses an Egyptian Royal
Cubit of 1.728 feet (20.736 inches), for a circumference of 24883.2 miles.
The outer rim of the Sarsen Circle at Stonehenge was 345.6 feet in circumference.
- 3.402 inches radius (6.804 inches diameter). There are 6804 days in the
lunar nutation cycle, major standstill to major standstill.
TOP POINTS @ 0 - 360-DEGREES.
- 2.9866666 inches radius (5.97333333 inches diameter). This is a special
ratio used for working in a compass circle of 56 positions (like the 56 posts
of the Aubrey Circle at Stonehenge) 56 ÷
2.98666666 = 18.75. The Great Pyramid's perimeter 3024
feet ÷ 2.9866666 = 1012.5 (a very useful lunar value). Application
of this ratio turns the perimeter of the Great Pyramid into a lunar or Sabbatical
Calendar calculator, based upon 56 positions (7 X 8...28 X 2). This station
on the lozenge would have been double coded to also mean 2.97 and relate to
readings in "11" series and "rounded PHI" (1.62) simultaneously
A combination of these values was encoded into the base dimensions of Menkaure
Pyramid. That pyramid had a design length of 356.4 feet or 12 X 2.97 feet.
The length also equates to 220 X 1.62 feet. The way the pyramid was designed
allowed it to be read in either rounded PHI (1.62) or "pure" PHI
(1.6180339) increments. The exact dimensional PHI ratio relationship that
existed between the Aubrey Circle and "Y" Holes at Stonehenge, also
existed between Menkaure Pyramid's side diagonal length to the apex and half
the base length (under the pure PHI assignment of 288 feet to 178 feet)...
178 X 1.6180339 = 288.
- 2.9333333 inches radius (5.866666 inches diameter). This relates to "11"
series navigation using the mile @ 5280 feet.
- 2.888888 inches radius (5.777777) inches diameter). This is a "13"
based progression used in calendar calculations. The Sabbatical Calendar ran
for 7 full years without correction, based upon 13 months of 28 days per year
(364 days). The solar cycle would be allowed to accrue 1.25 days of error
per year, which was corrected during a festival at the end of the 7th or Sabbatical
year. This station on the lozenge also codes 288, a foundation, multi-use
number of tremendous importance.
- 2.857142857 inches radius (5.714285714 inches diameter). This relates to
dividing up a 360 degree circle according to "reed" values (126
inches). 360 ÷ 126 = 2.857142857-degrees.
This value would be 5 degrees in a 630-degree compass, like the inner Sarsen
Circle rim at Stonehenge.
The right hand side of the lozenge is particularly laden with extra codes,
as a much magnified, high resolution photo of the lozenge will verify. Under
magnification it is seen that lines from separate quadrants, which should, technically,
intersect, don't do so but sit at staggered, extended points from each other.
Here is the result of assessing the positions within the exacting confines of
AutoCAD.
RIGHT SIDE POINTS @ 90-DEGREES.
- 3.571428571 inches radius (7.142857143 inches diameter). Again, this code
is not as difficult as it looks. It's merely the result of dividing 360 degrees
by 100.8. Under the Great Pyramid's "6&7" navigational system
100.8 feet represented 1 second of arc. The diameter of the inner Sarsen Circle,
rim to rim, through one section, was measured as 100.8 feet. This same station
on the lozenge would have also meant 3.564 inches and relate to the base length
codes of the Menkaure Pyramid (356.4 feet). The perimeter of Menkaure complied
to 54 divisions of 26.4 feet ("11" series). The lunar cycle counts
(2551.5 or 6804) also worked exceedingly well to 54 divisions.
- 3.54375 inches radius (7.0875 inches diameter). The sum of 354.375 days
is the length of the lunar year. The Khafre Pyramid had a design length of
708.75 feet (15/16ths the length of the Great Pyramid).
- 3.5 inches radius (7 inches diameter). This is simple "7" series
navigational or calendar coding, but would also have meant 3.52 inches radius
(7.04 inches diameter) and relate to "11" series navigation.
- 3.456 inches radius (6.912 inches diameter). Again, one of the dynamic codes
of antiquity, relating to the "6&7" navigational system found
on the Great Pyramid or the outer rim of the Sarsen Circle at Stonehenge.
- 3.42 inches radius (6.84 inches diameter). One of the Station Stones positions
at Stonehenge resides at 342-degrees, with another 180-degrees opposed at
162-degrees. This is suggestive of dividing a 360-degree circle into 20 positions
of 18-degrees each.
- 3.402 inches radius (6.804 inches diameter). This is in homage to the lunar
nutaion cycle of 6804 days.
- 3.375 inches radius (6.75 inches diameter). This value is part of a mathematical
progression used to track positions arrived at in the lunar cycle or Sabbatical
Calendar. The station would have been dual coded to also include 3.36 inches
radius and 6.72 inches diameter to provide useful values within the Great
Pyramid's "6&7" navigational system. There would be 15 X 6.72
feet in 100.8 feet (1 second of arc under the "6&7" system).
THE BOTTOM POINTS @ 180-DEGREES.
- 3.024 inches radius (6.048 inches diameter). The Great Pyramid @ 756 feet
per side has a perimeter value of 3024 feet. Twice the perimeter value (6048
feet) is 1 minute of equatorial circumference arc for the world under the
Great Pyramid's "6&7" geodetic assignment.
- 2.986666 inches radius (5.9733333 diameter). Again, the special ratio for
working in a circuit of 56 positions is encoded into this quadrant of the
lozenge.
- 2.97 inches radius (5.94 inches diameter). Again, the Menkaure Pyramid rounded
PHI and "11" series incremental readings are encoded into the bottom
stations of the lozenge.
- 2.933333 inches radius (5.866666 inches diameter). This ratio could be used
used to break circuits, based upon miles, into 1/18th segments. The station
would have been triple coded to mnemonically carry the values of 2.9166666
(5.833333 diameter) and 2.916 (5.832 diameter) inches, respectively, as well.
- 2.88888 inches radius (5.777777 inches diameter). If the Great Pyramid's
perimeter of 3024 feet is multiplied by 2.8888888 then the resultant value
is 8736, which is the number of hours in 364 days...the raw count figure used
in the 13 months, of 28 days each, solar year. This 364 day system was allowed
to run for 7 years without disruption, before correction, although some groups,
like the Hebrews, had a "double Sabbath" once a year to make the
annual count 365 days. This meant a correction (for them) of only 42 hours
at the end of each 7th year. Others simply made up the lost time at the end
of 7 years in a festival that added 8.75 days to the calendar count. This
station on the lozenge would have been dual coded to also mean 2.88 inches
(multi-use number).
TO THE ENDS OF THE EARTH.
Here in New Zealand, at the furthest reaches of the globe, an ancient purpose
placed tor mound, situated upon the northern ridge of the Waitapu Valley, sits
7000 Hebrew/ Celtic Royal Cubits from a laboriously carved, surveying "benchmark
cleft" on the sea cliff.. The azimuth angle from this equally ancient benchmark
cleft, to the southern face of the tor mound, is 51.84 degrees (the slope angle
of the Great Pyramid or azimuth angle through the centre of the huge Octagon
earth embankment complex of Newark, Ohio).
At the same time, the northern ridge tor mound centre sits 11520 feet from
the southern hubstone of the very impressive Waitapu standing stone observatory,
on an azimuth angle of 59.0625-degrees. Half of this value is 29.53125 and that
happens to be the number of days in a lunar year. The rising, diagonal face
length to the apex of Khafre Pyramid, under the 3,4,5 triangle rule by which
it was built, was 590.625 feet...half of which is the azimuth angle between
the centre of the northern tor mound and the huge hubstone at Puketapu Hill's
lower observatory site.
The line from the observatory to the northern ridge tor mound turns 120 degrees
and goes for 11520 feet to a standing stone marker on Puketapu Hill, where there's
another large observatory composed of about 200 cairns. At the Puketapu Hill
marker the line turns 120-degrees and runs for 11520 feet to the southern hubstone
of the Waitapu Observatory, forming a perfect equilateral triangle. The 11520
feet distance on each side of the triangle is .8 of a Geomancer's mile from
ancient Britain.
Another line extends for 12500 feet from the northern ridge tor mound to the
huge hubstone of Puketapu Hill's lower plateau alignment site. The azimuth angle
of this line is 295.3125-degrees, again accentuating the 29.53125-days in the
lunar month. Under the largest "10" series, ancient calibration, which
viewed the size of the Earth as 25000 miles of equatorial circumference, this
distance would represent 1/10560th part (2/5280ths).
If the 12500 feet were called miles, then this distance would mnemonically code
half of the equatorial circumference. A cairn, 100 feet beyond the hubstone,
marks a distance of 12600 feet from the northern ridge tor mound, or 1200 Hebrew
Reeds. This distance is 1/10368th or 2/5184ths
of the equatorial circumference under the Great Pyramid geodetic assignment.
The distance from the huge hubstone on Puketapu Hill's lower overland alignment
site to the southern hubstone of the Waitapu Observatory is 11340 feet, at an
azimuth angle of 172.8-degrees. The 11340 feet distance is a very prominent
lunar code. It is the exact distance equivalent of 15 sides of the Great Pyramid
or 16 sides of the Khafre Pyramid, on the Giza Plateau of Egypt. The 11340 distance
is in mnemonic reference to a day count interval within the 6804-day lunar nutation
cycle (major standstill to major standstill) wherein 1134-days equals 1/6th
of that period. The width of the Station Stones rectangle at Stonehenge is 113.4
feet. The azimuth angle of 172.8-degrees carries one of the most significant
navigational principles of antiquity in its numerical value.
Yet another line runs for 11520 feet from a giant, purpose place obelisk stone
near Puketapu Hill, to a yet larger tor mound on the southern ridge of the Waitapu
Valley...etc., etc.
There remain many coded stations on, especially, the Clandon Barrow Lozenge,
which this series of articles has neglected to analyse thus far. The Clandon
Barrow Lozenge, despite the fact that it's slightly smaller than the Bush Barrow
Lozenge, contains many more codes.
The truth against the world.

June 2003. ©

 .
.



