Ancient Universities NZ Part 1

For the New Zealand vernal equinox of 2020, we decided to turn our attention to the district of Raglan - Ruapuke on the North Island's West Coast and try to locate ancient, purpose built solar observatories in that region.
We knew that this coastal area of New Zealand had once been host to a huge, pre-Maori population and that they had left purpose-placed obelisks, surveying alignment markers and elevation calculating features in the local landscape, as well as large carved out hill structures.

Using Red Shift astronomy program, Google Earth, AutoCAD and some trigonometry, we calculated that the winter solstice sunrise would occur from an ancient, registered archaeological mound on the coast, so went with our cameras to document the event. The shoot was highly successful, and we were able to prove that the mound had been built to determine the exact day of the winter solstice, using the loftiest peak of Mount Karioi as the sunrise outer marker.

While in the Ruapuke district we heard about a long, highly excavated, flat topped PA structure that was marked by Tuahu stones on one of its purpose-built mounds.

Subsequent investigations indicated that the equinoctial sunset, as observed from the top plateau mound of the PA, would be onto tiny Gannet Island, 12.6-miles out to sea. A further deep reading of old archaeological reports seemed to suggest that this highly modified, long hill structure was probably an ancient Turehu wharewaananga or open-air university for teaching initiates special scientific knowledge. The tutorials would have been about cyclic astronomy, the lunisolar calendar system, stellar navigational principles ... coupled with positional plotting at sea, overland surveying for mapping, and readings of the equatorial circumference of the Earth under two navigational systems, etc.

Having done our homework, we vowed to return to Ruapuke and hoped to gain access to Manuaitu PA so that we could test our analysis at the vernal equinox in order to verify that Gannet Island was indeed the sunset position for an observer atop the PA.
The very name Rua-puke translates to “pit or hill upon a mound” and infers a surveying or observation trig or pit that an observer sits or stands in to view a location or event further afield. The term was anciently used in homage to a great, knowledgeable sage or priest of old called, Rua-te-pu-puke.

One name for the location of the PA, now called Manuaitu … (Bird of ill omen or calamity) was Korero-mai-waho, which translates to: The recounting of ancient wisdom on the open seaward coast.

The elongated, east-west ridge of Manuaitu PA on the Ruapuke Coast. All the indications are that this location was, in ancient times, an advanced school of learning or wharewaananga. The known presence of Tuahu (Turehu) stones, acknowledged in oral tradition history, would attest to this conclusion.

The compound name Korero-mai-waho seems to be the earlier title for the region, from a time of peaceful interaction and teaching before the latter era of calamity. The hill PA‘s name seems to have been changed after it fell to the Maori warriors and later into the possession of chief Te Rauparaha, the most murderous warrior-chief in New Zealand’s recorded history, who decimated and cannibalised tens of thousands of people, mostly throughout the northern part of Te Tau ihu o te waka (the top of New Zealand’s South Island).

The fact that Korero-mai-waho, in oral tradition, is said to have Tuahu stones infers that it was once an open-air-university or wharewaananga of the Turehu people, the conquered predecessors, annihilated by the Maori warriors.

One way to test this is to see if any “Rua-Puke” or “pits upon mounds” can be found that, in a dynamic sense, relate to a cyclic-astronomical or overland surveying function.

We were kindly allowed to go onto the site on the 20th of September 2020 (one day before the actual equinox) and quickly identified the solitary, central mound that had anciently been built to orientate onto the equinoctial sunset position. We later, in excellent viewing conditions, tracked the sun down to be aligned with Gannet Island’s northern edge at sunset's last glint. On the day after (the true equinox day) the sun would set slightly further south and be more fully on the small, sea-swept, rocky island.

We had verified that Gannet Island was the equinox outer marker from the purpose-built solar observatory.

A highly magnified view of windswept little Gannet Island, which sits due west of Manuaitu PA and represents the equinoctial sunset outer marker from the central observation mound.

Another magnified view of Gannet Island, taken from a more northern location around the coast.

The equinoctial sun with its glow diffused by wispy horizon cloud at the horizon, descended to Gannet Island and sank beneath the sea. Gannet Island marked the line to the setting position of the sun at the sea horizon. from the ancient wharewaananga.

We also turned our attention to the mound upon which the venerated Tuahu stones were placed, to see if any surveying-related attributes could be identified there. The 10.8-feet long, recumbent Tuahu stone had an arrowhead-like end pointing towards Mount Karioi.

The carved and terraced Tuahu mound, bathed in the last rays of the evening sun, overlooking Kawhia Harbour and Pirongia Mountain due east.

The carved, tiered top of the Tuahu mound, showing the 10.8-feet long Tuahu stone, with its arrowhead top pointing at Mt Karioi, the highest peak of which sits at due north.

A second fix to the east showed that the equinoctial sunrise would occur from the centre of Mount Pirongia. The evidence was clear that the mounds were built for accurate, 360-degree surveying and cyclic astronomical fixes, for keeping the calendar 100% correct.

The larger of two sandstone Tuahu stones on the top of the mound, shaped to have an arrow point at its northern end, lies recumbent in the grass on a north-south alignment, with east-west at 90-degrees to its length. Mount Taranaki situated 100-miles SSW can be seen from this elevated position.

A tuahu position, such as this, was referred to in oral tradition as a “listening post” … 'a place where the spirits and the gods could rest and be available for the benefit and welfare of the pa (village or fortified position) and its inhabitants'.
Under what was conceivably the former name of this location or district, Korero-mai-waho, the Tuahu hillock would be classed as a place of learning.

This seems to be further supported by the fact that there is no stream nearby and those gathered at or near the tall and short, Tuahu stone's listening post for ongoing instruction would need a support group to supply drinking or cooking water, food and other amenities.
Also, instructors or students at these open-air-universities were never permitted to have or eat food in near proximity to the Tuahu stones:

'Let this be quite clear: The tuāhu (or ordinary altar) is outside—not in the house. There are two (proper) sites for the tuāhu, one near the latrine, one by side of a tomb—those are the only proper sites. The reason of this is lest (the tuāhus) should be desecrated by the approach of food, or by food being suspended near them.'
See: The Lore of the Whare-wananga, chpt. 1, written down by H.T. Whata-horo, from the teachings of Te Matoro-hangi and Nepia Pohu-hu, priests of the whare-wananga of the East Coast, New Zealand. Translated by S. Percy Smith.

'In pre-European times the Maori had evolved a peculiar institution in the form of a school of learning. In order to preserve tribal lore it was necessary that it should be taught to a certain number of young men of each generation, hence the institution known as the whare wananga or whare kura.

Each tribe of importance contained certain men skilled in tribal history, in long conserved myth and ritual.

To these men were given the task of transmitting the prized lore to young men selected as pupils ... The teaching of all these tapu (sacred or secret) matters was necessarily itself and extremely tapu business and no person not engaged in either teaching or learning was allowed to be present.

In some cases instruction was given at some secluded spot away from the village; in others the lessons were conducted in a house that was put under tapu and to which the public had no access at the time.' ...
In his settlement of Polynesia, the Maori was compelled to dwell in isolated, far-sundered communities and then each one had to preserve its own lore as best it could.
Some communities seem to have succeeded much better than others.

In New Zealand the institution was kept up faithfully by the principal tribes and we have the names of many of the old houses. The Takitumu folk of the eastern side of the North Island were perhaps the most advanced in regard to this mode of preserving knowledge.

Some of the whare wananga were famous for many generations, such as "Ra-wheoro" at Uawa.

In such cases the actual house was rebuilt when it fell into disrepair, for it was not a Maori custom to repair a house.
In other cases, the whare wananga was but a name and a system; no special house bore the name and the knowledge pertaining to it might be taught in the open air or in any house set apart for the purpose.'
See: The Maori As He Was, by Elsdon Best, pp. 84 - 85, Government Printer, Wellington, 1932.

For a more comprehensive account concerning the lore and practices of the whare wananga institution, see:
The Lore of the Whare-wananga, written down by H.T. Whata-horo, from the teachings of Te Matoro-hangi and Nepia Pohu-hu, priests of the whare-wananga of the East Coast, New Zealand. Translated by S. Percy Smith.

Here is a picture of the Crosshouse of Miringa te Kakara, the last know surviving whare-wananga building of the Takitumu people of the Central North Island, seen here in disarray before being burnt down in 1983.

It's exact positioning on the landscape and measurable geometric features show that many surveying and astronomical features were built into its position, dimensions and angles, such as the 3,4,5 triangle.
Photo courtesy of Jan & Ron Raison.

One replacement outer wall slat of timber, undoubtedly from a 19th century renovation, was measured by this author. It was found to have surprising measurement and angle attributes. These included encoded 3,4,5 triangles at each end, meaning it sat on the wall at an angle of 53.130-degrees, the same as the slope angle for an outer face of the Khafre Pyramid of Egypt.

The 3,4,5 triangle is of extreme importance to carpenters laying out the foundations of a building in order to ensure the corners are perfectly square.
If the diagonally angled outer slats were purely decorative, the majority of carpenters or architects would be more likely to set the angle at 45-degrees, but not so in the case of the Crosshouse. Each slat was code-bearing in terms of lengths and angles and contained profound tutorials.

Taylor’s drawing of what the Crosshouse looked like when in pristine condition. The crossing wings had slightly different design attributes, as can be seen in the pointed or rounded, wide vertical fascias at the porches.

This building was the last known wharewaananga, school of learning, to survive in New Zealand.

It is said to have been established by the Pao-Mirere or Hau movement at Miringa Te Kakara in the centre of the North Island as a building dedicated to the cult of IO.

There appears to be some confusion, however, as to the date of the original building's construction, as well as disagreement amongst the Maori tohungas (sages) as to whether or not Pao-Mirere activity, related to the "Crosshouse", was to construct an entirely new building or simply to renovate an older existing structure.

It is known that a series of wharewaananga buildings, bearing the name Miringa Te Kakara or Waerenga A Kakara, had existed for centuries. Similar "temple" structures were located at 3 other close-by centres contemporary with the era of the Crosshouse. The name is said to have been an ancient Hawaiki one (original homeland), also rendered Miria te Kakara in some dialects.

One historical quote states: ‘It is wrong to describe Miringa te Kakara as an “offshoot of Pai-marire” or the centre of a “new religion”. Miringa te Kakara was one of four Io cult centres.

Other similar temple structures in the district were: Whenua-tupu on the Waimiha stream, about three miles north-east of the Waimihia railway station; Papaawaka on the Ongarue River about one mile above its junction with the Waimiha stream; Kete-maringi or Hurakia, on the Hurakia Range at the headwaters of the Ongarue River.

The building, initiated by King Tawhiao's directive to Chieftainess Ngaharakeke, is said to have been completed in about 1865. Bishop Thomas Herangi, guardian of the Crosshouse up until the 1980's, cited oral history evidence of the cruciform-shaped star temple as having been built in 1682, with renovations occurring in 1788 & 1887.
For further information see: http://www.celticnz.co.nz/Crosshouse/Crosshouse1.html

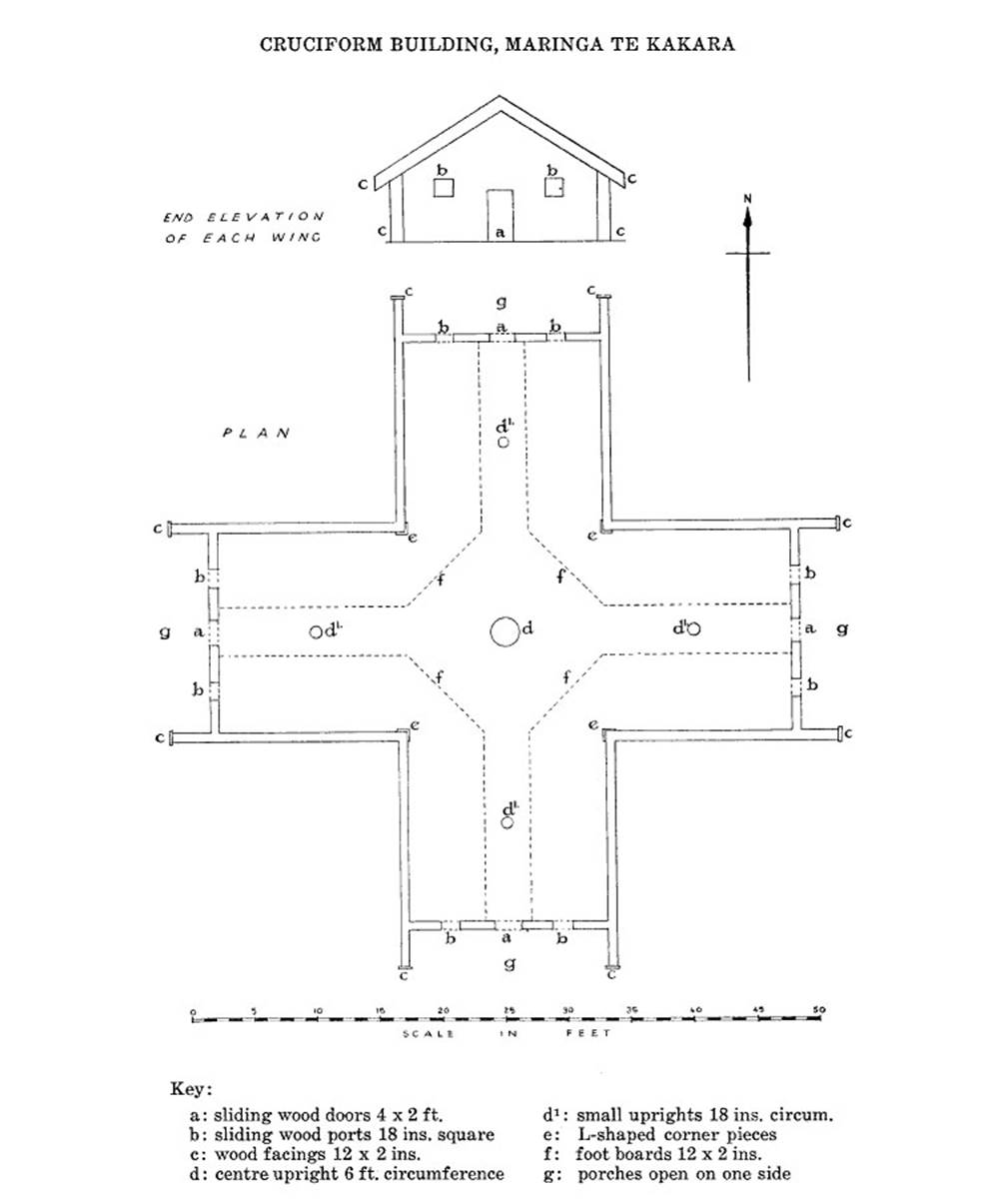
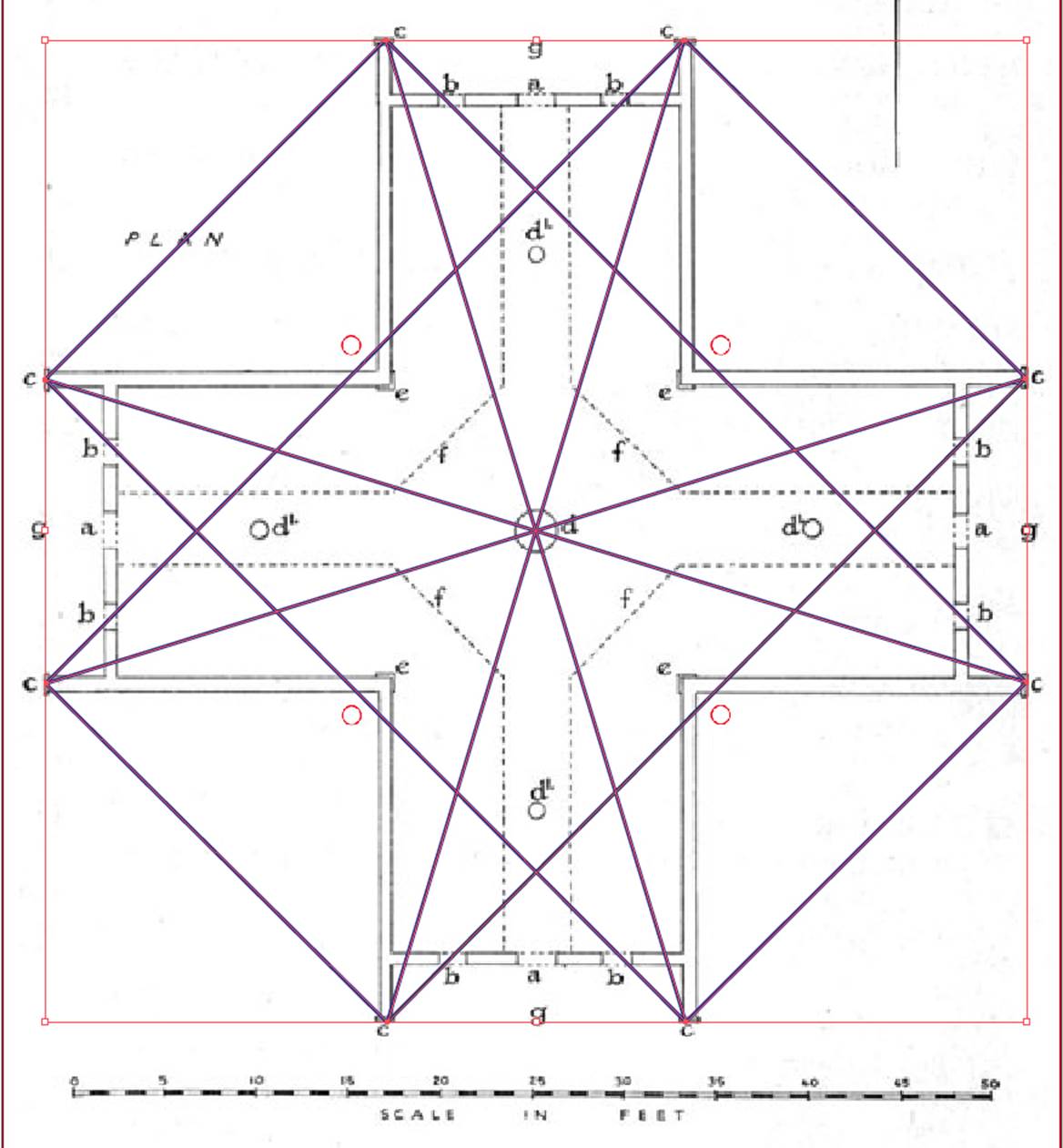
In the year 1958, a quarter of a century before a Maori arsonist, hearing voices in his head, torched the building, archaeologist-surveyor CG Hunt did a careful survey of the Crosshouse building and drew this scaled plan.

Thankfully, his careful work has preserved for posterity the ground-plan dimensions and the plan can be tested to see if the placement of walls, the internal platform path, posts & corner L-shaped moldings or extremity porch facing boards, etc., comply to code-bearing measurements and ‘old-world’ geometric patterns of known pedigree.

Over the years several publications have mentioned measurements of the Crosshouse, like the 1959 Journal of the Polynesian Society article, which gives the following description:

'This building is 54 ft in length along the north-south and east west axes. Each wing is 17 feet wide and the height to the ridge poles is 11 ft. 6in.
Each wing has a small open sided porch and entrance to each is gained through a sliding door hewn from one piece of timber 4 ft high, 2 ft wide and 2 ins. thick...Each portal is fitted with two ports to admit light and these are closed by solid wooden slabs about 18 ins. square and 2 ins. thick, which are slid into position....The walls...are about 6 ft. high. Inside the building will be seen 5 uprights, which have been set in the ground to support the ridge poles...the centre pole is about 6 ft. in circumference while the other 4 are 18 ins. in circumference. At the inner corners of the cruciform structure are some L-shaped corner pieces 2 ins. thick... About 6 ft. in from each wall are footboards about 12 ins. wide and 1½ ins thick.'

Hunt's scaled plan has been used in this mathematical-geometric analysis of the Crosshouse.

The orientation of the Crosshouse of Miringa te Kakara was 30-degrees counterclockwise off true north, east, south or west. This means that two wings pointed towards the 60-degree winter solstice sunrise and 240-degree summer solstice sunset, whereas the other wings pointed towards 330-degrees and 150-degrees, respectively.

Just exterior to the corners, where each wing begins, it was found during my survey in 2001 of the remains, that there were four more small charred post stumps that Hunt had omitted to include.in his 1958 plan. In the pictures that follow the four additional post positions are marked as red circles.

SO, WHAT SURVEYING ATTRIBUTES DOES THE CROSSHOUSE OF MIRINGA TE KAKARA SHARE WITH MANUAITU PA … KORERO-MAI-WAHO?

The Crosshouse was built in such a way that the centre pole within the house used the peak of Mount Ranginui as its true north outer marker, in the same way that the Tuahu mound of Manuaitu PA used the peak of Mount Karioi to fix onto due north.

The highest northerly peak of Pureora Forest Park Range, 12-miles to the east, was the rise position of the equinoctial sun, just as the centre mound of Manuaitu PA orientated onto the rise position of the equinoctial sun from Mount Pirongia or the set position onto Gannet Island.

It’s significant that when the Takitumu Maori people moved to the central North Island district (Tiroa) they met the Patu-paiarehe or Turehu people and lived peaceably alongside them for many generations. Much later, when hostilities arose, probably due to the influx of less friendly tribes, the Patu-paiarehe people had to flee into the vast high country of Pureora Forest Park and the Rangitoto Range. However, oral tradition history shows that the Takitimu people, or many in their midst, wished to maintain close contact with the vanquished Patu-paiarehe and kept the former, now abandoned star-temple in a good state of repair, replacing, piece-by-piece, any deteriorating parts.

For this constant renovation procedure, a defective part had to be carefully removed intact, then used as a template for duplicating the replacement part. This was done to religiously preserve the inbuilt codes, counts, angles and measurements of every part of the cruciform structure, all of which carried a profound meaning and associated tutorials.

All the evidence shows that the Crosshouse of Miringa te Kakara, also called a star-temple or the temple of the four winds, was originally a Patu-paiarehe structure.
‘It was in these temples, colleges, or houses of learning, that the priests of old taught the young men of their particular tribes, with the constant admonition never to depart from what they learned, nor to allow other subjects than those taught by the tribal priests to be introduced into the colleges.

The Sage states that youths from other tribes might be taught therein; in which probability he means the series of tribes of the East Coast who all, more or less, are related to the descendants of the crew of the "Takitimu" canoe that came here about 1350, and also to the original tangata-whenua people, about whom we shall learn later. It would seem from the difference in the teachings found in other tribes that this is so’.
See: The Lore of the Whare-wananga, written down by H.T. Whata-horo, from the teachings of Te Matoro-hangi and Nepia Pohu-hu, priests of the whare-wananga of the East Coast, New Zealand. Translated by S. Percy Smith.

THE CODE-BEARING MEASUREMENTS, STAR & CROSS GEOMETRY, PHI & PI CODING, FOR TEACHING NAVIGATION, CYCLIC ASTRONOMY OR THE LUNISOLAR CALENDAR SYSTEM.

In analysing code-bearing edifices of the great civilisations of antiquity, from the pyramids of Egypt to Stonehenge to New Zealand, and everything in between, it’s important to realise that there was, universally, one very sophisticated, standardised unit of measurement in use.
It will be surprising to many to find out that all of the cubits or other named measurements were based upon the self-same inch and that unit of measurement is now known as the British Standard inch, which is not British at all, but stems from much earlier, more remote civilisations of antiquity.

As an example, the Great Pyramid of Egypt, in its original pristine condition, was architecturally designed to be 756 English standard feet (9072-inches) for the length of one side. This equates to exactly 720 Greek feet, 360 Assyrian cubits, 72 Hebrew reeds, 440 Egyptian Royal cubits, 800 Egyptian feet (unit identified by Herodotus in consultation with Egyptian priests … 5th century BC), 432 Celtic or Hebrew Royal cubits, 504 Celtic short cubits, 540 old kingdom Hebrew cubits of a man, etc.

A close analysis of the most ancient Mediterranean, Continental European or British Isles measurement standards shows they were all using the same inch, despite the fact that small errors of drift crept into their old, more precise measurements over centuries of time. Although the preferred cubit, foot or mile of one cousin nation might vary in length to that of another, they were all intended to be in perfect ratio, one with another.

Indeed, 19th century American archaeologist, J. Ralston Skinner, who undertook precise surveys of Ohio's geometric earth mounds, came to the same conclusion. Skinner, after years of on-site analysis stated that the mound builders of the Ohio Valley had positively used the increment known as the British standard inch in the design and construction of the ancient geometric earth mound complexes he surveyed.

See: Skinner, J. Ralston. "Identification of the British Inch as the Unit of Measure of the Mound Builders of the Ohio Valley." Journal of the Cincinnati Society of Natural History Vol. 9 (July 1886), pp. 51-63.
This journal can be accessed online by going to: Cincinnati Historical Society Digital Journals

It can be added that the angle calculating standard in North America, in antiquity, was the Sumerian 360-degree system and this holds true for ancient structures over several continents all the way to the ends of the earth in New Zealand.

Please keep it in mind that in the following geometric, measurement and angle related system, built into the Crosshouse of Miringa te Kakara, nothing would work if a wall was moved, a porch shortened, or the internal raised pathway lengths and angles changed, etc.
The building was the repository of codes, based upon measurable lengths and angles and the same numbers generated are found encoded into ancient edifices from Egypt to New Zealand.

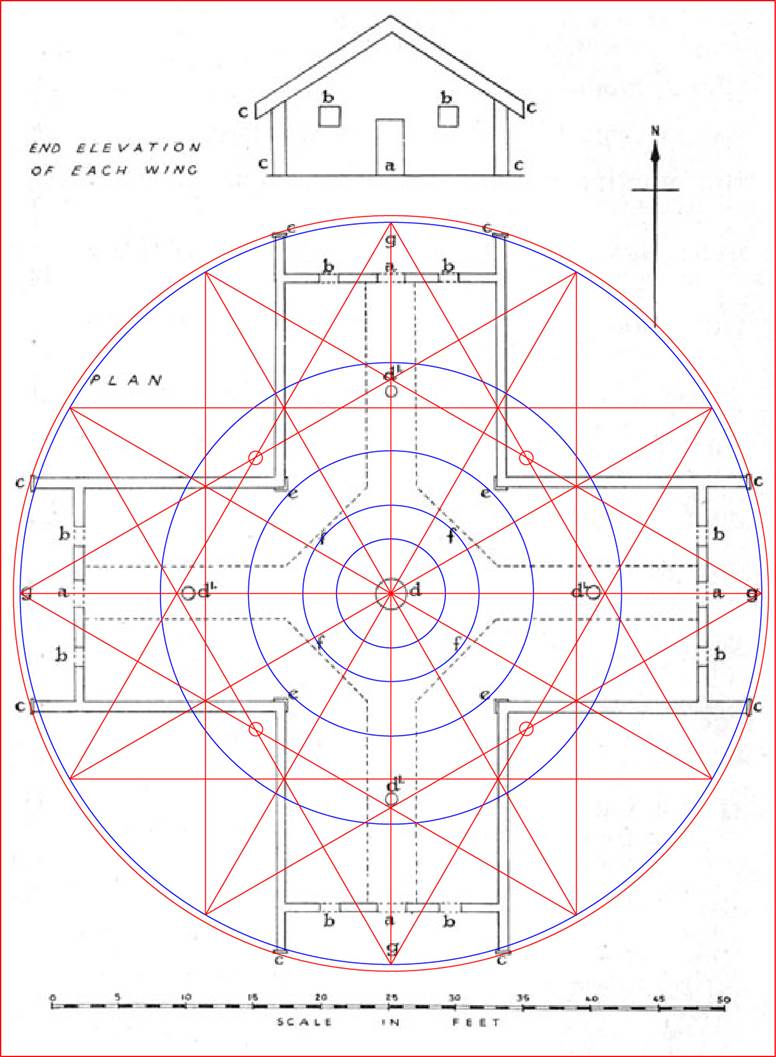
12-pointed star is the star of the zodiac constellations, which sit 30-degrees apart around the ecliptic or equatorial sweep of the Earth. As the world rotates around its axis, completing one full rotation every 24-hours, it is facing one of the 12 constellations for 48-minutes, whether in daylight or night.

Alternatively, as the Earth revolves around the sun over the 365.25-day year, it sits within the 30-degrees wide zone or segment of the sky of a particular zodiacal constellation for 12.175-days (292.2-hours) before drifting into the zone of the neighboring zodiacal constellation.

Each 91.3125-days (91 & 5/16ths) the Earth will arrive at one of the four cardinal points of travel, namely, the summer solstice, autumnal equinox, winter solstice and vernal equinox. These are the landmark days for which solar observatories were built by ancient societies that identified the exact day of the cardinal solar event. These milestone, annual events occur as the Earth is positioned around the sun in the segments of sky allotted to the constellations, Aries, Cancer, Libra, or Capricorn.

If the zodiac star within the Crosshouse (as above) was depicted as a 6-pointed star, then there would be star points orientating onto north and south, whereas two other star points would point towards the winter solstice rise and set positions. The remaining two-star points would orientate onto the summer solstice rise and set positions.

This holds true in sub-tropical countries like New Zealand, where the sun’s movement between solstices spans about 60-degrees of horizon travel. At more northern or southern latitudes, the solstice star points would need to be spread slightly wider to fix accurately onto the true or actual solstice rise and set positions.

For an understanding of just how geometrically sophisticated and code-bearing this precise floor plan actually is, consider the following:

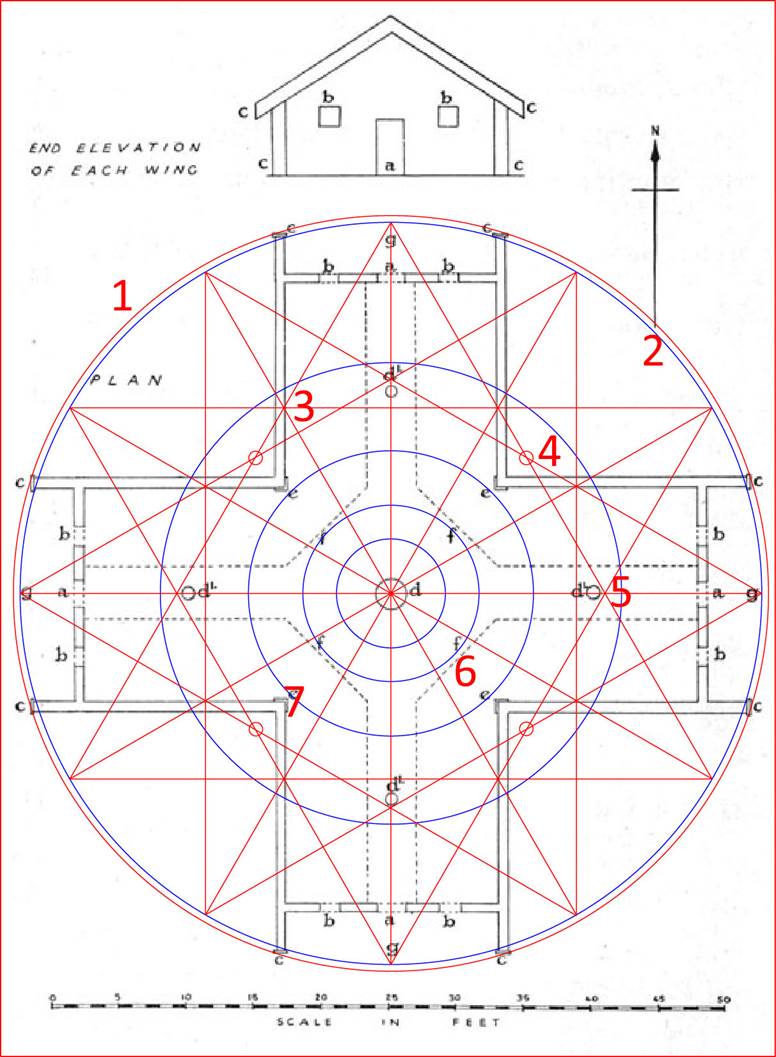
Position 1: This outer circle sweeping the extremities of the cruciform building is 56-feet in diameter and brushes the outer face of the vertical fascia boards. This circle, in its circumference, is coded to provide a mathematical progression related to the mile of 5280-feet and navigation using increments of length based upon that mile. This family of otherwise ancient increments (based upon the number 11), continues to be used into modern times and is composed of:

7.92-inches (the link), 5.5-feet (the old merchant navy fathom …still used into the 20th century), 16.5-feet (The rod or perch … 3-fathoms), 66-feet (the chain), 660-feet (the furlong or furrowlong), 5280-feet (the mile … 1760-yards), 16500-feet (the ancient league …3.125-miles … 3 &1/8th -miles).

Patupaiarehe students at the Crosshouse would have been taught several ancient renditions of the PI ratio for specific use in achieving whole number readings of circumferences when using number strings or families as diameters of circles. These included: 22/7 or 1728/550. Other, slightly less accurate values included 3.15 to 1 or 3.125 to 1.

The 56-feet diameter circle X PI @ 22/7 = 176-feet and a mathematical progression based upon this value goes:
176, 352, 528, 704, 880, 1056, 1232, 1408, 1584, 1760 … 2112 … 2640 … 5280 … 6336 … 7920 … etc.

Of course, 1760-feet is 1/3rd of a mile. The value 7920-miles was the number used from ancient times to describe the diameter of the Earth. This fact is easily determined in consideration of the mathematical codes built into the Great Pyramid of Egypt to divulge the equatorial circumference of the Earth.

Position 2: This slightly inwards circle that brushes the inner face of the vertical fascia boards is 55-feet in diameter. Of course, 55-feet is 10 merchant navy fathoms or 1/96th of a mile. One could theorise with confidence that a third circle was symbolically represented on the outrigger walls of the Crosshouse’s porch, that had a sweep of 52.5-feet in diameter. This would have introduced yet another dynamic navigational system that was encoded into the literal base dimensions of the Great Pyramid of Egypt, as well as Silbury Hill in Southern England (a purpose-built hill erected in circa 3000-BC using chalk blocks). 52.5 X PI @ 22/7th = 165-feet.

One cross measure of the slightly elliptical base of Silbury Hill was 550-feet, whereas 90-degrees opposed the cross measure was 525-feet.

The ancient Greek system of overland travel measurement or for navigation at sea (positional plotting), adopted by them from the Egyptians, used a mile of 5250-feet, which was 30-feet shorter than the 5280-feet mile. A diameter of 52.5-feet would be 50 Greek feet of 12.6-inches each. Increments under the Greek system were divisible by the numbers 6 or 7.

12.6-inches (1 Greek foot), 5.25-feet (1/2 a Hebrew reed), 10.5-feet (10 Greek feet or 1-reed), 525-feet (short stadia or stadium), 630-feet (long stadia or stadium), 5250-feet (5000-Greek feet or 1 Greek mile).

A Greek mile of 5250-feet converts to a circumference of one English league when multiplied by PI @ 1728/550. Thus, it becomes 16500-feet or 550-inches per degree of arc on the circle. These principles of converting sea-leg diameters to circumferences easily divisible in a 360-degree circuit environment were essential to positional plotting upon the featureless oceans, beyond sight of landmarks.

It was important that every ensuing generation of the Patu-paiarehe students be trained up concerning the navigational knowledge carried by their forefathers from the Northern Hemisphere to New Zealand in antiquity. Thus, the wharewaananga of Miringa te Kakara, as well as several others in the district … and seemingly many more locations across New Zealand.

Position 3: Note how triple converging lines of the crossing geometry denote the exact spacing between the inner walls. This occurs at 8 positions of the Crosshouse with severe exactitude. If the design was such that the walls were at slightly altered spacings, this star geometry would be off-line and not work.

Position 4: In my survey of the Crosshouse remains in 2001, I found 4 additional charred posts that sat external to the corners of each wing. Their positions were measured in relation to the centre post stump and I added them to Hunt’s plan of 1958. It can be seen that each post relates to the crossing geometry of the 12-pointed star.

Position 5: Just as the external corner posts are markers for the 12-pointed star geometry, so too are the internal posts that jut up from the walkway platform, midway through each wing. The converging geometry brushes the sides of these 4 posts and the crossing point of the vectors determines the measured limit from the centre-post that they must not exceed.

Position 6: In the above picture the inner blue circles are each a reduction by the PHI ratio (1.6180339 to 1) of the outmost blue circle (55-feet diameter). The same could have been done starting at the outmost circle (56-feet in diameter). Such a reduction of the slightly larger red circle would create an inner circle that determined the outer limits of the pathway ramp at the centre of the building (3rd reduction).

Position 7: The slightly larger outer circle (red … 56-feet diameter) in its 2nd PHI reduction would brush the nosing on each of the 4 internal corners.

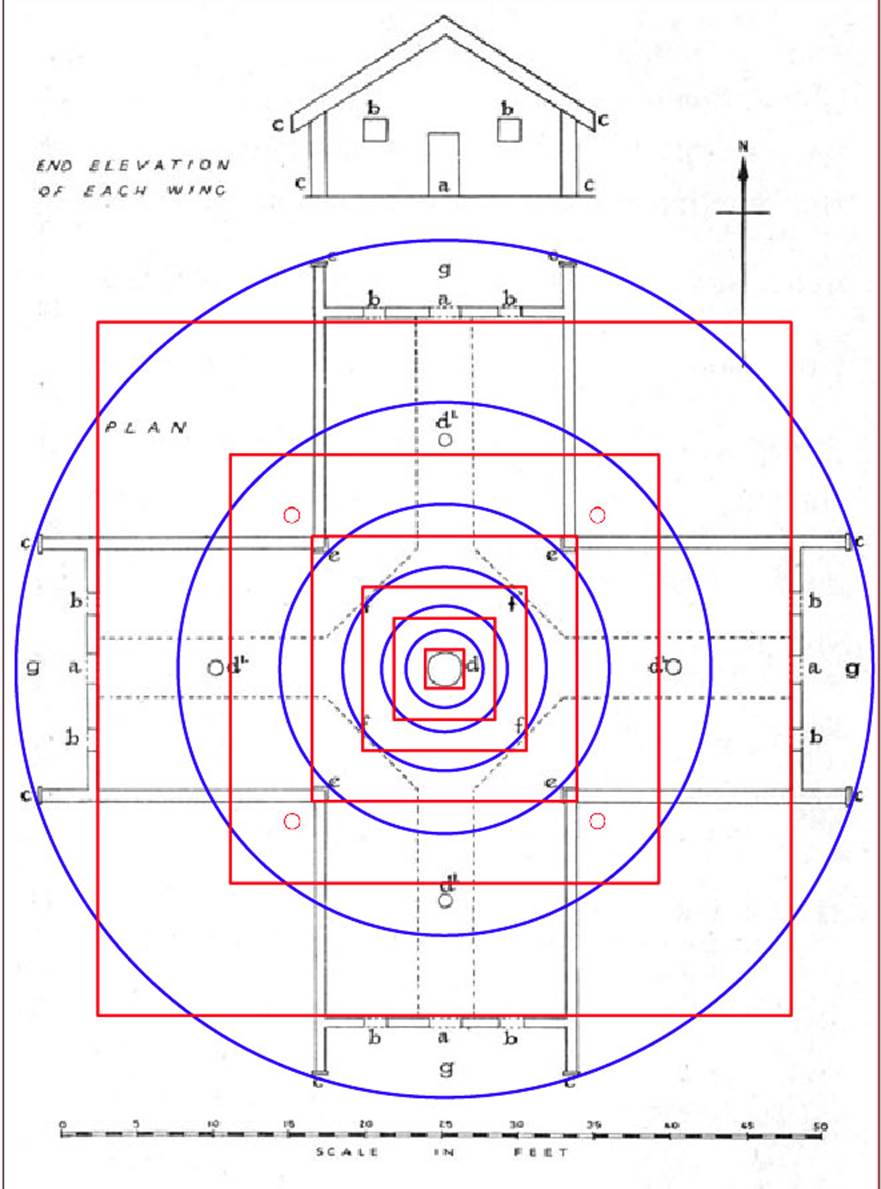
Ancient mathematicians were preoccupied in encoding the PHI ratio, as is evidenced within the dimensions of the Crosshouse. The outer circumference of a circle encompassing the building (56-feet) is reduced by ½ PHI (.80901695) and a square is produced based upon that result. It can be seen that the square reasonably fits the internal limits of each wing at the door thresholds.

The 2nd inwards, PHI reduced concentric circle is then divided by ½ PHI to create the next overlaying square … & no significant “hit” is identifiable in this circle and square reduction. However, the 3rd inwards circle sweeps the noses of the internal corner moldings and the square produced from the ½ PHI reduction of that circle corrals the corner moldings and defines the outer width of the wings. Again the 4th inwards PHI circle extends to the limits of the internal, central walkway.

The use of the PHI ratio was highly important to the ancient civilisations and was encoded into both the Great Pyramid of Egypt and in the PHI reducing circles of Stonehenge of Southern England.

Position 1. From the centre of Stonehenge an outer-marker boulder marked “B” sits a coded radius of 233.28-feet away on the Avenue. This distance was also read as 233.3333-feet. The measured value sets up a mathematical progression that goes:
233.28, 466.56, 699.84, 933.12, 1166.4 …1866.24 …5832 … 6531.84 … 93312 … 11664 … 130636800.

This mathematical progression codes the equatorial circumference of the Earth under the same navigational system that is found in the literal dimensions of the Great Pyramid’s base (756-feet per side). Therefore, one circumnavigates the Great Pyramid twice (8-sides) to achieve 6048-feet (1-minute of equatorial arc). This value is then multiplied by 60 to arrive at the distance of 1-degree of equatorial arc (6048 X 60 = 362880-feet). Again, this distance is multiplied by 360 to arrive at a full equatorial circumference of 130636800-feet or 12 X 12 X 12 X 12 X 1.2 so-called Greek miles of 5250-feet each (5000-Greek feet) or 24883.2 Greek miles.

Remember, the fledgling Greek civilisation acquired their system of metrology in consultation with the Egyptians and other old civilisations.

In the above line-up of numbers is 93312. The Babylonian Talent weight was 933120-grains. One also sees 11664 and the Roman foot was 11.664-inches. One also sees 5832 and the Roman Pace measurement was 5 Roman feet or 58.32-inches. It’s significant that the ancient Druidic bronze plaque called the Calendar of Coligny is 58.32-inches in length, or 1-Roman pace.

Inwards from position 1 is a blue circle that defines the extremities of the main, central Stonehenge complex and encompasses the entire circular site (except the Avenue and Heel stone). It is slightly elliptical but is coded to represent 384-feet in one cross measure.

Position 2: One now reduces the code bearing diameter of this circle (466.56 or 466.66666-feet) by the PHI ratio (1.6180339 to 1) to arrive at a coded 288-feet diameter of the Aubrey Circle, with only miniscule error. Therefore, 466.56 ÷ 1.6180339 = 288.35-feet. A mathematical progression based upon 288 goes:

288, 576, 864, 1152, 1440, 1728, 2016 … 2592 … 3456 … 5184 … 6048 … 6912 … 7776 … 10080 … 10368 … 15552 … 25920 … 31104 … 36288 … 124416 … 248832 … 130636800.

A mathematical progression based upon 288 is one of the most dynamic of antiquity, producing very significant numbers that relate to the equatorial circumference of the Earth. The progression divulges numbers attributable to seconds (100.8-feet), minutes (6048-feet) and degrees of arc (362880-feet … 69.12 Greek miles).

At Stonehenge, the 30 lintels atop the Sarsen circle averaged 11.52-feet* each on the outer faces, or 345.6-feet of circumference. The sum of 3456-miles would be 1/72nd of the 24883.2-mile equatorial circumference of the Earth and the 345.6-feet circuit of the Sarsen Circle outer face would be 1/378000th of the 130636800-feet equatorial circumference. Note: half the side length of the Great Pyramid is 378-feet.

*Note: C.G. Hunt, in speaking of height of the Crosshouse stated: “the height to the ridge poles is 11 ft. 6in”. The intended code would have been 11.52-feet or a little less than 1/4th of an inch greater than 11 ft. 6in.

Also, the value 25920 occurs in this string. The Precession of the Equinoxes endures for 25920-years or 72-years X 360. The outer face of the Heel Stone at Stonehenge sits a coded distance of 259.2-feet from site centre.

The value 10368 is also in the line-up and in the 24883.2-mile equatorial circumference reading, the Earth spins at 1036.8 MPH in 24-hours. Significantly, the Hebrew Desert volume standard for liquids, called a Cab, was 103.68 cubic inches, as was the Stirling Jug volume of old Scotland … etc., etc.

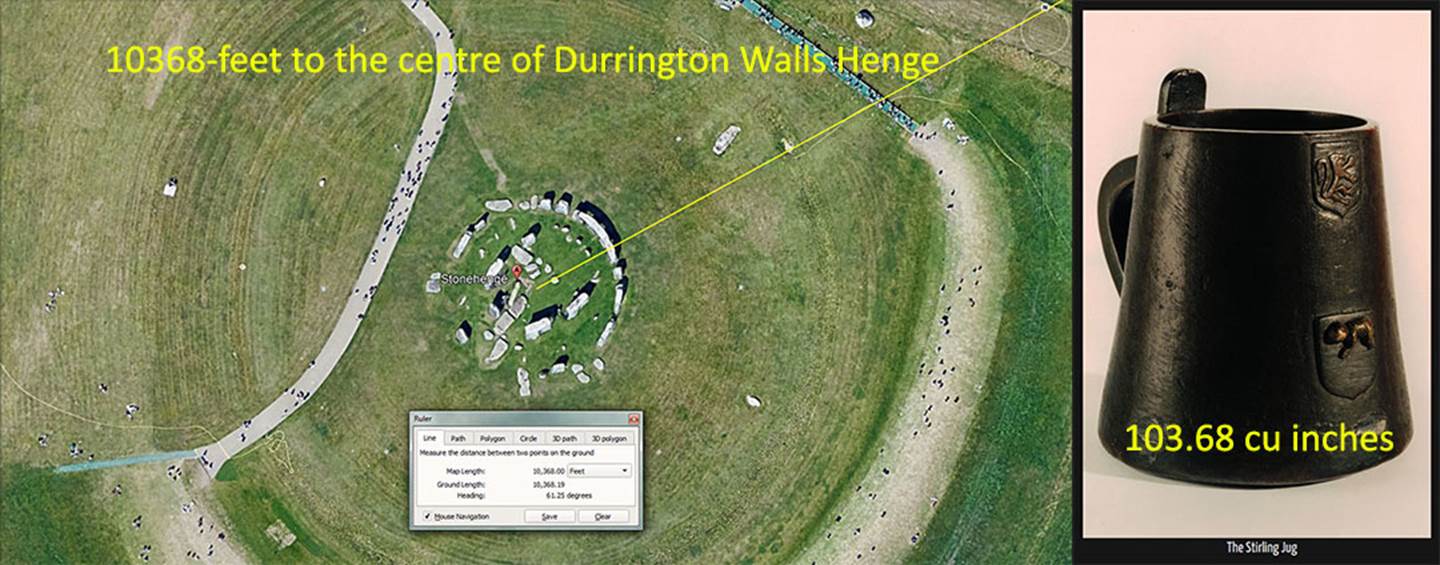
The apparent coded distance of Stonehenge from the centre of Durrington Walls Henge is 10368-feet or 6000 of the largest of 3 Egyptian Royal cubits @ 20.736-inches each. This distance is also 124416 inches, and half the equatorial circumference of the Earth was coded to be 12441.6-miles under the Great Pyramid’s literal base dimensions. This segment of Earth measure, running between the centres of Durrington Henge (the cathedral) and Stonehenge (the chapel) is 1/12600th of the 24883.2 Greek mile equatorial circumference (130636800 English feet … or 124416000 Greek feet of 12.6-inches each).

Position 3: The “Y” Holes Circle is a PHI reduction of the Aubrey Circle and is coded to be 178.2-feet in diameter. Therefore, the Aubrey reduction by PHI achieves 178.21-feet.

Under a second navigation system, using the mile of 5280-feet, the Earth was configured to be 24750-miles in equatorial circumference.

This string accentuates navigation by the ancient Scottish mile of 5940-feet, which was 1-furlong (660-feet) longer than the English mile. It is very evident that measurement increments of 2.475-inches or 2.475-feet were used on Megalithic-Neolithic sites. The "Y"-Holes Circle @ a diameter of 178.2-feet is 864 increments of 2.475-inches or 72 increments of 2.475-feet (29.7-inches). Note, the half value of 5940 is 2970.

Inwards from “Y” Holes another blue circle is shown. This is the “Z” Holes Circle and it’s 132-feet in diameter or 1/40th of an English mile of 5280-feet or 1/45th of a Scottish mile of 5940-feet.

Position 4: This is a PHI reduction of “Y” Holes circle. Thus, 178.21 reduces to 110.13. The code infers 110-feet running on the lintels of the Sarsen Circle. One cross measure of the inner face of the Sarsen Circle lintels is 100-feet, whereas the slightly elliptical circle achieves 100.8-feet 90-degrees opposed. The 100-feet diameter was undoubtedly for tutorials concerning the various forms of PI generated in the circumference reading, including 22/7ths; 1728/550ths, 3.15 (1/2 a Greek long stadia was 315-feet) or 3.125.
The 100.8-feet cross measure of the inner Sarsen circle, 90-degrees opposed, is 1-second of equatorial arc. Therefore 100.8-feet X 60 X 60 X 360 = the Earth’s equatorial circumference of 130636800-feet or 24883.2 Greek miles.

The PHI ratio is also fully encoded into the Great Pyramid of Egypt in the following way:

If one uses simple trigonometry to work out the side length of the full pyramid, including the theoretical, non-existent capstone, the length to the centre apex would be (Adj. ÷ 51.84 Cos.) = 611.7894615 feet.
Alternatively, if one used a PHI method of Adj. (378 feet) X PHI (1.6180339) = 611.6168142 feet.

It will be observed that the calculated PHI length is only about 2 inches less than the length achieved by straight trigonometry. The ancient astronomer/ mathematicians were coding a PHI related angle for the Great Pyramid simultaneously to the standard angle of 51.84-degrees. The whole edifice was designed to clearly code PHI relationships.

Let's consider the Great Pyramid on the basis of PHI and the ratio relationship (in pyramid acres) between the 4 faces, compared to the ground area that the Great Pyramid covers.
The surface area of each face of the theoretical full pyramid, complete with a (symbolic) pointed capstone, = 611.6168142 feet of side length X 378 feet (1/2 the base length) = 231191.11558 square feet.

Because there are 4 faces, their combined square footage amounts to 924764.6231 square feet. This translates to 32.10988275 pyramid acres of 28800 square feet each.
The base area measured 756 feet X 756 feet or 571536 feet, which equated to 19.845 pyramid acres of 28800 sq. ft each. A perfect PHI relationship exists between this (symbolic capstone included) total side acreage and that of the base: 32.10988275 ÷ 19.845 = 1.6180339 (PHI).

Trigonometry dictates that the Great Pyramid’s height, including a capstone (which has never been seen on the structure in all recorded history), would have achieved 481 & 1/11th feet, to a very close tolerance, where the 4 lines, coming up from the face sides, connected at the apex point.

With the Pyramid length being 756-feet per side, two sides equal 1512-feet. The sum of 1512-feet ÷ PI @ 22/7ths = 481.090909-feet (481 & 1/11th -feet).

The earliest Zodiac designs of the Middle East were laid out within two overlapping rectangles or a cross, in much the same design configuration as the Crosshouse of Miringa Te Kakara.

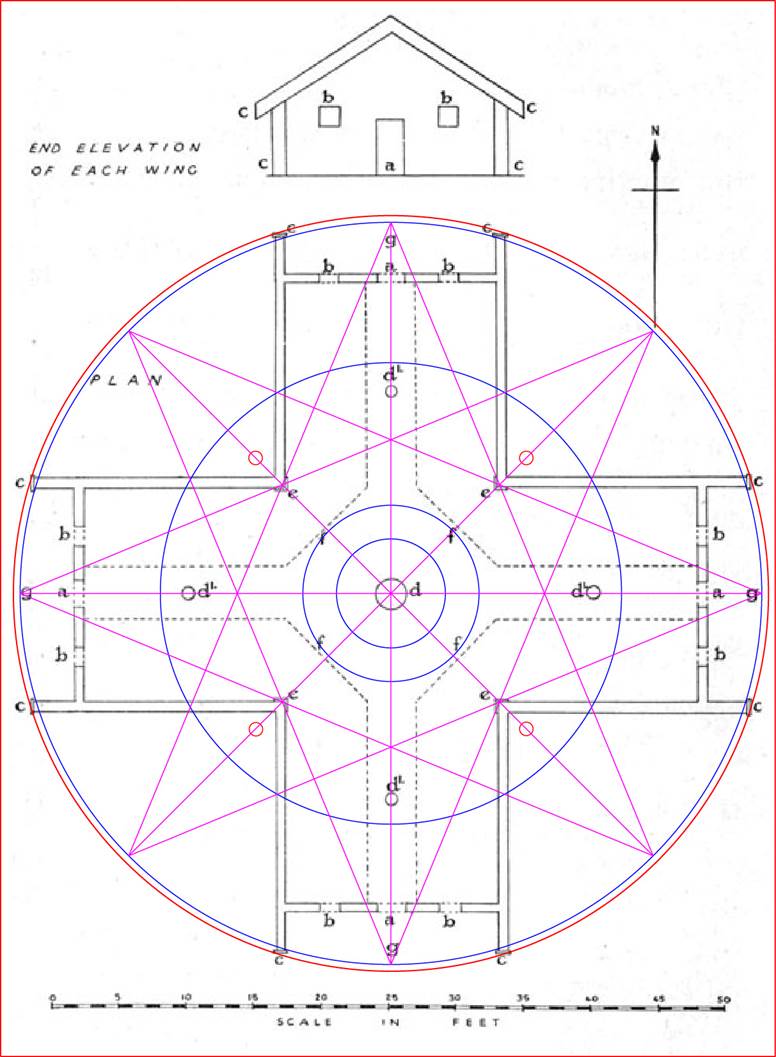
The 8-pointed star geometry fits perfectly within the architectural confines of the Crosshouse. It was used by ancient savants to mark the primary and secondary points of the 360-degree compass. With star points on north and south, the east and west star points oriented onto the equinox sunrise and sunset positions of the horizon.

Note how intersecting vectors tuck into the edges of the internal corner moldings or dissect the face corner, before crossing the outside posts. Four star points pass centrally through the outer doorways.
Use of 8, 16, 32, etc., divisions within a 360-degree environment has been the common compass-reading practice since remote antiquity, spanning thousands of years.

Amongst the venerated symbols of ancient Northern Hemisphere civilisations was the Grand Cross, here depicted within the Crosshouse.

Note how diagonal vectors pass through the window openings or designate where the internal walkway turns to traverse each wing.

Depicted here is the 14-pointed star or two overlaid “Stars of the Typhon” (the 7-pointed star). This design, as either 7 or 14-star points, was much used in ancient calendar calculations or counts. Thus, we have the ancient agrarian or peasant calendar, known as the Sabbatical Calendar, that ran for 7 solar years before intercalary days were inserted during a 9-day festival correction at the end of the Sabbatical Year (7th year).

The Sabbatical Calendar was composed of 7-days in a week, 14-days bi-weekly, 28-days in a month and 13-months in a year (52-weeks). This smooth running, non-disruptive system accrued 1.25-days of error per annum, culminating in 8.75-days of error by the end of 7 solar years.

The system was very convenient for a lunisolar calendar system that tracked the positions of both the Earth around the sun and the moon’s position around the Earth simultaneously, using the number 7.
The lunar year is 354.375-days (about 11-days shorter than the solar year) and the moon’s most important long cycle, called the lunar nutation cycle, was configured by ancient astronomers to endure for 6804-days.

At Stonehenge, the Aubrey Circle is composed of 56-post positions and the 6804-day lunar cycle could be counted out between post positions in 121.5-day increments (2916-hours). Unsurprisingly, the 2916-hour value, if put into a string, produces a progression we have already dealt with:

2916, 5832 … 11664 … 23328 … 46656 …72900 … 93312 … 653184 … 130636800.

Remember, the Roman pace was 58.32-inches and their foot was 11.664-inches. The large circle at Stonehenge, extending to boulder “B” on the Avenue from site centre, has a radius of 233.28 or diameter of 466.56-feet. The value 7.29-inches is found to be the length of the Bush Barrow Lozenge artefact from Stonehenge (dating to about 2500 BC or so). The sum of 7.29-inches is also 1/8th of a Roman Pace … and these increments were in use on British sites a couple of thousand years before there was a Roman civilisation.

In addition, 933120-grains was the ancient Sumerian-Babylonian Talent weight; 65318400-feet is half of 130636800-feet (the equatorial circumference of the Earth under the Great Pyramid’s navigational assignment (24883.2-Greek miles).
In the above picture, note how vectors conjunct with the internal, vertical corner moldings, define the limits of the central platform around the centre post, relate to internal post positions or windows, etc. This star pattern would have been very important to lunisolar calendar related tutorials.

A series of near squares are seen to overlay each wing of the Crosshouse, extending from the outside walls to the vertical corner molding inside faces, and to the porch exterior threshold of the doorways. Small discrepancies occur due to some of Hunt’s lines meandering slightly offline or falling slightly short, whereas the individual squares, generated in AutoCAD, are fashioned to precise coded measurements.

Architect-archaeologist C.G. Hunt stated: “Each wing is 17 feet wide” and in a coded sense this is very significant. The Patu-paiarehe builders would have wished to mnemonically achieve 17.01-feet (17-feet and 1/9th of an inch) for the following reason:

With each of the 4 wings being 17.01-feet wide, the total of 17.01 X 4 = 68.04-feet and this coding is in homage to the 6804-day lunar nutation cycle, monitored within the ancient lunisolar Sabbatical calendar system.

Whereas the sun goes to its most extreme positions up and down the horizon in the course of 365.25-days, it takes the moon 18.613 solar years to move from Lunar Major Standstill to Lunar Minor Standstill, then back again. The actual time involved is 6798.36-days, but this is not a factorable number that the ancient astronomers could break down easily, so they settled on a calculation span of 6804 days that was fluidly divisible … (only about 6-days of error in over 18.6-years).

The ancient savants obviously knew that the gravitational tug of the moon upon the Earth, its oceans and atmosphere, was the largest determiner of weather. Extremes could occur when the Earth was at critical points around the sun and the moon at critical points around the Earth. The moon’s position could portend times of famine or abundance and had to be monitored closely as a predictor of coming weather.

Whereas the outside to outside width of the wings was coded to be 17.01-feet, the distance from the face of the inner corner vertical moldings to the outer door threshold appears strongly to have been mnemonically set at 16.180339-feet (coding the PHI ratio). This could also have been read as 16.2-feet to represent a “rounded” form of the PHI ratio widely used in ancient code-bearing edifices. A mathematical progression based upon 162 goes:

162, 324, 486, 648, 810, 972, 1134, 1296 …1944 … 2592 … 4536 … 5184 … 5670 … 5832 … 6804 … 7290 … 9072 … 10368 … 11664 … 12150 … 25920 … etc.

Note how the diagonal crossing vectors tuck in snugly against the pathway poles of each wing.

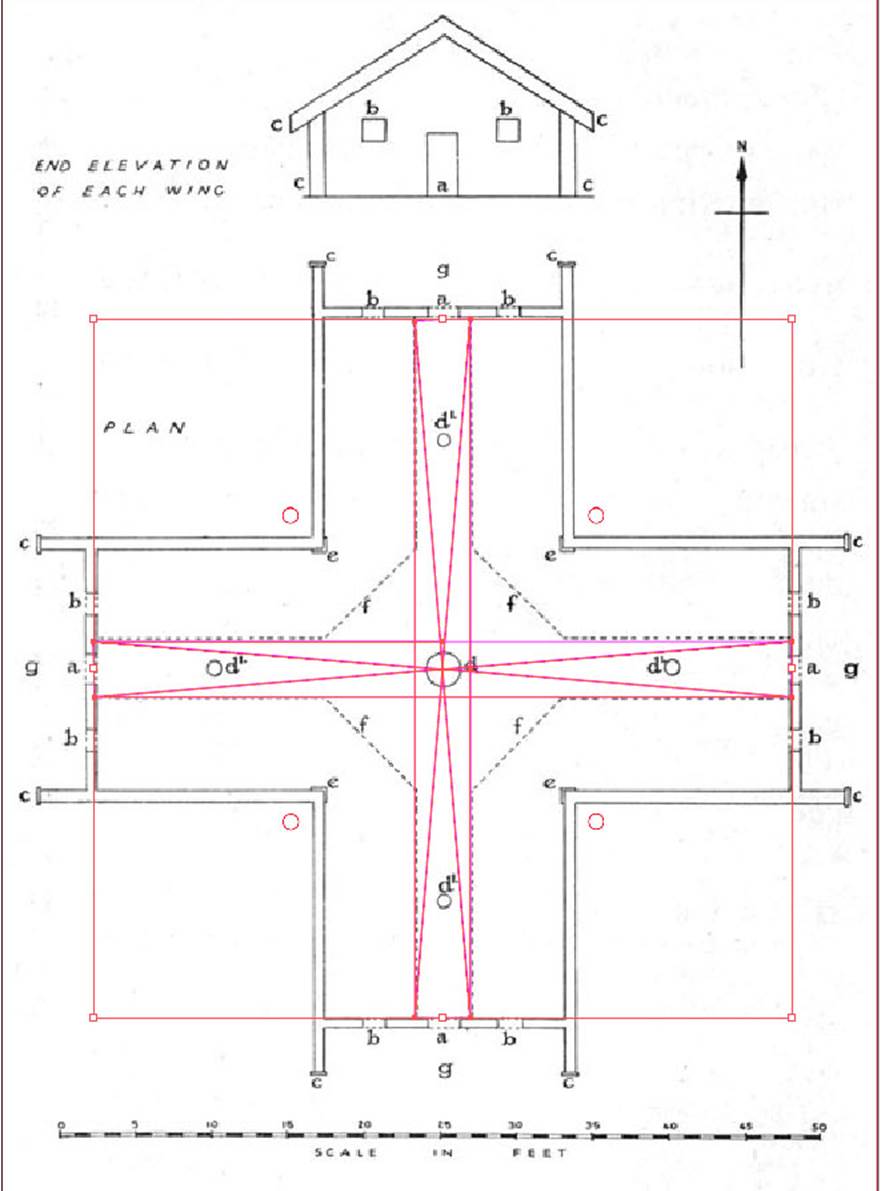
A coded length running from inner threshold to inner threshold in a cross pattern was the thin Cross of Set, so-called in some quarters. This one measures 46.08-feet in length X 3.6525-feet in width (3 & 21/40ths) for each 90-degrees opposed cross-bar.

460.8, 921.6, 1382.4 …2304 … 4147.2 … 6912 … 10137.6 … 11520 … 12441.6 … 24883.2

This progression relates to the navigational system that configured the Earth to be 24883.2-miles of equatorial circumference.

The width aspect of each cross bar has been sized to fit the central pathway and is 3.6525-feet (3 & 21/40ths ). There are, of course, 365.25-days in a solar year.

In the above scaled picture, created in AutoCAD, circles emanate out from the posts of each wing and touch the inner walls of the Crosshouse. Each circle has a diameter of 15.708-feet. This value X 2 = 31.416-feet and the PI ratio is 3.1416 to 1.

The inner walls, in their distance between opposed faces, encoded the numbers related to PI and tutorials would have identified the various, proximity forms of PI used for whole number circumference readings when calculating number families. For calculating the “6 & 7” number families, used in what became Greek navigational increments of length, the form of PI used was 22/7ths . For calculating using the “11” family of numbers, in what became the English navigational increments of length, the form of PI used was 1728/550ths . Other slightly less accurate forms used were 3.15 to 1 & 3.125 to 1.

Note how the circles extend to the inner doorway threshold or define the edge position of the central walkway platform where the circles intersect.

In the above picture all of the circles have a diameter of 15.708-feet and each crossing wing, extending to the outer doorway thresholds, attains 47.124-feet of length or PI @ 3.1416 X 15. To achieve this layout, one would have used a fulcrum position on the outer side of the wing posts, facing the doorways.

Where the blue lines intersect with the touching PI encoded circles, the straight pathways into each wing are seen to begin from the diagonal running sides of the centre platform.

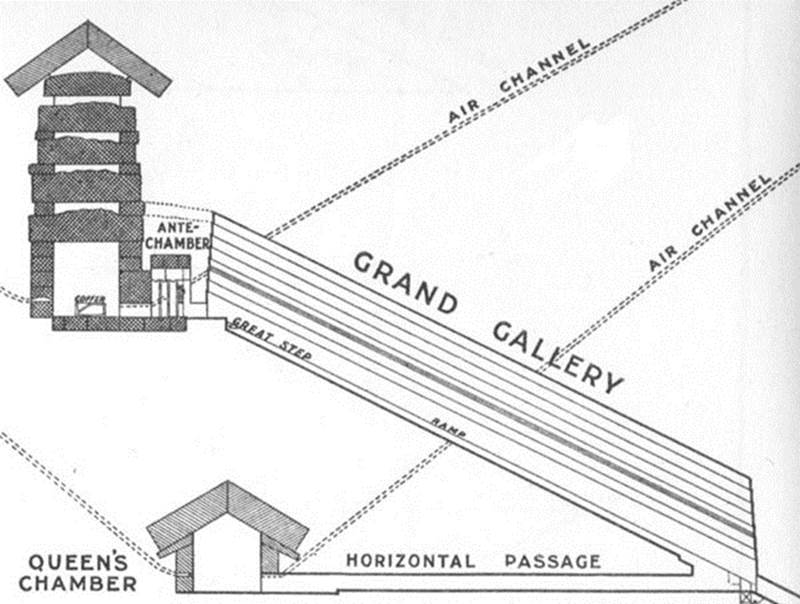
The 15.708 feet internal width of the Crosshouse is duplicated, at increased ratio, in the length of the Grand Gallery within the Great Pyramid. Sir William Flinders Petrie, using one of the newfangled steel measuring tapes that had recently been invented, measured its overall length as 157 feet. Petrie wrote:

'Returning now to the gallery from which we diverged to the Queen's Chamber, the length of the gallery was measured like the other passages, with the steel tape. The total length on the slope is 1883.6, (inches) or 1815.5 (inches) to the face of the great step at the southern end ; and the average variation from a straight line is .15 in the sides, and .5 in the floor, which is somewhat curved down in the middle.'

Knowing that the more major lengths and angles of the Great Pyramid carried in-built codes, one naturally assumes that the original builders of the pyramid’s grand gallery intended to encode 157.08 feet into this length (less than an inch more than 157-feet). Similarly, such expressions of coded PI are found at Stonehenge and at the Octagon geometric earth embankment complex of Newark, Ohio, USA, etc., etc.

In tutorials at the Crosshouse of Miringa te Kakara, the outer-threshold-to-outer-threshold distance across 2 consecutive wings would also, symbolically, have been read as 47.25-feet (3-inches longer overall) for the following reason:

One of the variations on the PI ratio, used in ancient calculations, was 3.15 to 1, and this value was prominent in what became Greek metrology, where their half stadia measurement was 315-feet (300 Greek feet)*.

Under this slightly enlarged rendition of PI, the 3 PI circles stretching through each of the double wings would be considered as 15.75-feet each in diameter, for a length of 47.25-feet overall (45 Greek feet).

This increment determined the base lengths of both the Great Pyramid and Khafre Pyramid of Egypt, where the Khafre Pyramid (Egypt’s pyramid of the moon) was 15/16ths the length of the Great Pyramid. Therefore, 756 -feet ÷ 16 = 47.25 … X 15 = 708.75-feet (… the length of the Khafre Pyramid and 675 Greek feet).

*It is worthy to note that one diameter measurement across the slightly elliptical, inner Sarsen Circle at Stonehenge was 100-feet. This was obviously for tutorials about the various versions of PI when working in particular number families. If using 3.15, then the circumference would be ½ a Greek long stadia or ½ the length of the sprint running event at Olympia.

The above picture shows how the equatorial circumference of the Earth, under the 2nd navigational system, was symbolically or literally, encoded into the base perimeter dimensions of the Great Pyramid of Egypt. All it would have taken is to mark an extra 3-inches onto the paving slab perimeter at the base corners.

The overlapping rectangles seen above form a cross, and further diagonals within the rectangles form a Maltese or Templar cross standing upright.

The important measurement information is that the length of each rectangle is 49.5-feet and the width is 26.25-feet. A number string derived from the length value encodes the navigational system that used the miles of 5280-feet or 5940-feet. .
It will be seen that the rectangles relate perfectly to the exterior fascia boards of the Crosshouse building on each wing in this scaled overlay of Hunt’s plan (completed within the exacting confines of AutoCAD).

The length feature of the rectangles provides a mathematical progression that relates to the Scottish mile of 5940-feet, extending to the full equatorial circumference @ 24750-miles of 5280-feet or 22000 Scottish miles. Therefore, we have:
49.5, 99, 148.5, 198, 247.5, 297 …396 … 594 … 792 … 1188 … 5940 … 7920 … 24750 …130680000.

In this line-up, 5940 is the Scottish mile; 7920-miles is the diameter of the Earth; 24750-miles of 5280-feet is the equatorial circumference, equating to 130680000-feet.

If the Great Pyramid was read to be 756.25 feet in length (3-inches longer), then a whole new navigational system would occur using the “11” series of navigational increments based upon the mile of 5280 feet. Under this system, 1-minute of equatorial arc would be 6050-feet (instead of 6048-feet under the Greek mile method); a degree of arc would be 363000-feet and the full circumference 130680000 or 24750 English miles (22000 Scottish miles).

Alternatively, the width measurement of the rectangles, @ 26.25-feet, relates to the navigational system that used the so-called Greek mile of 5250-feet … 30-feet shorter than what became the English mile of 5280-feet and 690-feet shorter than the Scottish mile of 5940-feet. The 26.25 progression goes:

26.25, 52.5, 78.75, 105 …157.5 … 315 … 420 … 472.5 … 525 … 630 … 708.75 … 2835 … 5250

In this line-up 10.5-feet would be 1 Hebrew reed or 10 Greek feet; 315-feet would be ½ a Greek long stadia; 472.5-feet would be the design height of the Khafre Pyramid of Egypt under a 3,4,5 triangle formula; 525-feet would be a short stadia; 630-feet would be a long stadia; 708.75-feet* would be the base length of the Khafre Pyramid; 2835-feet would be the perimeter length of the Khafre Pyramid (4-sides) and 5250-feet would be a Greek mile.

*Note: 708.75-feet is 354.375 X 2 … and there are 354.375-days in a lunar year. The Khafre Pyramid was 15/16th the length of the Great Pyramid …756-feet ÷ 16 = 47.25 … X 15 = 708.75-feet.

In this picture the Crosshouse is shown in its correct orientation 30-degrees counter-clockwise around from due north. The position of due north, from the Crosshouse centre pole, resolves to the apex crown of Mount Ranginui 10.5-miles away and accurate compass bearings were easily attainable as a result.

The two overlapping rectangles were coded to measure 43.2-feet long by 21.6-feet wide.

For tutors wishing to provide foundation numbers from which highly significant mathematical progressions could be initiated, the opportunity would not be missed to mention proximity, special numbers at each code-bearing station. In the case of 43.2-feet, one could also mention the attributes of 43.75-feet … or in the case of 21.6-feet, one could mention the code-bearing mathematical attributes of a string based upon 22-feet, etc.

432, 864, 1296, 1728, 2160, 2592, 3024, 3456, 3888 … 5184 … 6048 … 6912 … 7776 … 9072 … 10368 … 11664 … 13824 … 15120 … 19440 … 20736 … 25920 … 31104 … 124416 … 248832.

This dynamic progression relates to the 12 X 12 X 12 X 12 X 1.2 – mile equatorial circumference of the Earth and incremental values within that string.

The length 3024-feet is the distance around the Great Pyramid @ 756-feet per side; 345.6-feet is the intended design circumference of Stonehenge’s outer rim Sarsen Circle and 345.6-miles would equate to 1/72nd of the equatorial circumference; 5184 reeds of 10.5-feet each is the area that the Great Pyramid covers at is base (72 X 72 square reeds) and the slope angle of each face is 51.84-degrees; 6048-feet is 1-minute of equatorial arc; 69.12 miles is 1-degree of arc; 9072-inches is the length of the Great Pyramid; 1036.8-MPH is the speed the 24883.2-mile Earth spins in 24-hours; 11.664-inches was the length of a Roman foot; 151.2-feet was very close to Petrie’s 2nd measurement of the Grand Gallery ‘to the face of the great step at the southern end’ and 1512-feet is the length of 2 sides of the Great Pyramid; 20.736-inches (1.728-feet) was the length of the largest of 3 Egyptian Royal Cubits identified by Petrie; 25920-years is the duration of the Precession of the Equinoxes (5184-years X 5); 3110.4-miles is 1/8th of the equatorial circumference whereas 12441.6 is ½ and 24883.2 the full circumference under the Great Pyramid’s literal base perimeter length assignment.

Alternatively, a mathematical progression based upon the width of the above rectangle within the Crosshouse goes:

216, 432, 648, 864, 1080, 1296, 1512, 1728, 1944, … 2160, …25920 … 248832.

Of interest is the fact that 2160 cubic inches was the original volume of the old English bushel and the sun spends 2160-years in each House of the Zodiac during the 25920-year cycle of Precession. Also, the diameter of the moon is 2160-miles and the diameter of the sun is, essentially, 864000-miles.

Looking due North towards outlying buildings from the Crosshouse. On a clear day Mount Ranginui and its summit radio tower would be seen above the gap between the buildings in this 1983 photo.

One of the surviving “Nui” poles that sat a coded distance away from the Crosshouse. These were used to align the building when it was under construction.

To the right of the picture are two more “Nui” pole stump markers bracketing a small implement shed. These sat at coded distances and angles from the thick centre pole at the Crosshouse centre.

The present distribution of surviving posts seems to indicate the following codes:

Posts @ 60-degrees azimuth and 240-degrees azimuth, which were intended/coded to lie 68.04 feet centre to centre from the central pole of the Crosshouse. The degree of error is 5.5 inches excess (60-degrees) and 4.3 inches shortfall (240-degrees). This distance codes the 6804-days of the lunar nutation cycle.

From the north-eastern doorway, one would witness the winter solstice sunrise and, from the southwestern doorway, the summer solstice sunset.

Posts @ 150-degrees and 330-degrees, which lie 72 feet from the epicentre of the Crosshouse. The degree of error is 14 inches shortfall at 150-degrees and 12 inches excess at 330-degrees. This is a dynamic, much used increment in ancient astronomy and navigation, with the inch total for the whole range (144 feet) amounting to 1728. Note: there are 1728 cubic inches in a cubic foot and the circumference of Silbury Hill in Southern England is 1728 feet, based upon a diameter of 550-feet. An ancient form of PI was 1728/550ths .

Posts @ 60-degrees, 240-degrees and 330-degrees, which appear to have been intended to form a symmetrical square around the Crosshouse (one missing), using ropes extending to the rear of the posts. The square would have achieved 151.2 feet per side, for a perimeter value of 604.8 feet. One side of this square would have been exactly 1/5th of a base side value of the Great Pyramid. The total perimeter value of 604.8 feet would be 1/10th of 1 minute of arc (6048 feet) under the sexagesimal geodetic system. The degree of error depends upon the original thickness of the posts, but assuming 18 inches of thickness the present error would be about 6 inches shortfall per post. The coding might have been related to a square of 150 feet per side or 600 feet perimeter, which would also have provided calibration for compass tutorials or 3,4,5 triangle computations, etc.

Posts @ 240-degrees and 330-degrees appear to have once been components in a square (two posts missing) with sides of 198 feet, for a combined perimeter total of 792 feet. This square would have served the purpose of providing calculations related to the size of the Earth under the "11" series (league) geodetic system, which used leagues, miles, furlongs, chains, rod/ perches, fathoms and links. Under that system the Earth was 7920 leagues in circumference and 7920 miles in diameter. The degree of error in the placement of the post at 330-degrees appears to be about 6-inches and in the post position at 240-degrees, negligible.

In the above summary of a few inches here and there of shortfalls, it’s probably useful to consider that, just like at Stonehenge, the original posts would have rotted over a century or so and needed replacement. Latter individuals undertaking maintenance might not have been 100% zealous in doing accurate restoration of the precise positions of the posts. This could happen when individuals were not sufficiently trained in the lore and codes of the wharewaananga.

“Pureora, the domed mountain towering over it, was the last refuge of the Patupaiarehe or fairy people. The house, Cowan asserts, was built to maintain contact with them”.

THE GREAT OPEN-AIR UNIVERSITIES OR SCHOOLS OF LEARNING OF BRITAIN & CONTINENTAL EUROPE

The New Zealand whare-wananga institution is virtually identical to the druidic institution of pre-Roman Britain. As Julius Caesar said, concerning the Druids of Britain in his day:

'They do not think it proper to commit these utterances to writing, although in all other matters and in their public and private accounts they make use of Greek characters. I believe that they have adopted the practice for two reasons- that they do not wish the rule to become common property, nor those who learn the rule to rely on writing and so neglect the cultivation of memory; and, in fact, it does usually happen that the assistance of writing tends to relax the diligence of the student and the action of memory...They also lecture on the stars in their motion, the magnitude of the Earth and its divisions, on natural history, on the power and government of God; and instruct the youth in these subjects' (see De Ballo Gallico, VII, 15, 16.).

The late era Druidic schools that Julius Caesar commented about, undoubtedly, had a pedigree back to similar schools maintained during the Neolithic and Bronze Ages.
British historian, Isabel Hill Elder, commenting on the Druidic schools, writes:

'The students at these colleges numbered at times sixty thousands of the youth and young nobility of Britain and Gaul. Caesar comments on the fact that the Gauls sent their youth to Britain to be educated...It required twenty years to master the complete circle of Druidic knowledge. Natural philosophy, astronomy, mathematics, geometry, medicine, jurisprudence, poetry and oratory were all proposed and taught-natural philosophy and astronomy with severe exactitude' (Elder refers to Strabo I IV, page 197. Caesars Comm. Lib V. Sueotonius, V Calegula. E. Campion, Accounts of Ireland, pg. 18.).

We now know several locations around New Zealand where there were open-air universities or Great Schools of Learning in New Zealand’s remote antiquity. The ancient institution persisted part way into the Maori epoch and a form of Maori wharewaananga carried on for a time. The earlier tutorials that accentuated navigation, surveying, cyclic astronomy, calendar computations, weights-measures & volume standards or mathematical principles carried from the Northern Hemisphere, were replaced by Maori religious cosmology, oral traditions, myths & legends or studies of magic & maketu (spells & curses). It seems that the very sophisticated sciences, encoded by numbers, were lost when the Patu-paiarehe people fled to the high hinterland to escape annihilation.

Thankfully, the Crosshouse survived reasonably intact into the mid-20th century, sufficient for archaeologist-surveyor CG Hunt to measure and record its dimensions for posterity. From this we are able to see what would have been taught to the brightest and the best of initiates at Schools of Learning distributed elsewhere across the length and breadth of New Zealand, including Manuaitu PA - Korero-mai-waho at Ruapuke, Raglan. The code-bearing buildings that were once erected there are now utterly eradicated beyond trace and only scant alignments remain, including equinox rises and sets or a north fix onto the summit of Mount Karioi from the Tuahu stones.

Several years ago this author was told by Maori kaumatua (elder), Graham Tatana, that his ancestors encountered long-term inhabitants that they called “The Surveyors” upon arriving in New Zealand. According to Graham, these earlier people were pre-occupied with marking the landscape with surveying stones, trigs or purpose-built sites all across the country. This observation is substantiated by a Hillsborough, Auckland, NZ resident whose great-grandfather was a leading surveyor in the 3rd quarter of the 19th century. In his diary he had recorded how, very often upon arrival at a suitable site for a surveying trig marker, he would see the clear marker-stone evidence of more ancient surveyors who had preceded him to mark the spot.

These strategically placed, ancient surveying trigs are easily found over the length and breadth of New Zealand and many of them function as both solar observatories and simultaneously a “fix” onto one of the primary points of the compass (due north, south, east or west). Here’s an example:

At the Waitapu Valley, situated on the northern side of Maunganui Bluff, Northland, New Zealand is a large, ancient standing stone circle on the seacoast cliff. This was a part of a sprawling open-air university that contained many purpose placed surveying markers extending over surrounding hills and valleys. The above photo was taken shortly before sunrise on the day of the equinox.

To the left side of the picture the long, horizontal Tutamoe range is seen in the distant background that extends to a “V” trough in the landscape (centre). At the declining end of the range is Tutamoe Mountain. To the right of the picture is the near-in Maunganui Bluff hill range and on it can be seen a purpose-built tor-mound hump, which served several solar observatory or overland alignment surveying functions from different locations around the district.
The base of the “V” trough, formed by the two declining ends of the ranges represents due east (90-degrees) from the centre of the Waitapu standing stone circle, so was the target for getting accurate degree angle fixes from the centre of the site to anywhere else around the horizon.

Ancient astronomer-surveyors knew that the equinoctial sunrise on the eastern sea coast would be at 90-degrees (due east) or at the centre of the trough, but also knew that the sun had to climb up on a diagonal angle to the north and wouldn't’t emerge into view until it had climbed through considerable terrain. It would therefore make its “first glint” on the top of the Tutamoe Range some distance to the left (north) of the “V”.
This is the equinoctial sunrise spectacle one witnesses from the centre of the standing stone site:

The first glint of the sun is in a slight dip depression atop the range and a resident astronomer, well acquainted with the local terrain, would know the “first glint dip ”outer-marker that heralded the rise of the equinoctial sun.

The Waitapu standing stone circle sits on a seaward cliff in full, constant view of the sea horizon and at an easily measurable distance above the high tide mark.

At Maunganui Bluff, Northland, New Zealand there is much purpose-placed, ancient stonework (obelisks, cairns) throughout the Waitapu Valley and on the slopes or crown of the high bluff itself. Likewise, there are many sighting pits for surveying and, in this photo, the foreground terrain has a dual hubstone, standing stone circle, many component boulders of which are of an impressive size.

From the central region of the standing stone circle the "V" in the skyline (left), where the lower end of Maunganui Bluff declines down to conjunct with the background (darker haze) Tutamoe Range, the degree angle around from true north is 90-degrees. The "V", sitting at true east, therefore provided the ancient surveyors on the standing stone site with a fix reference onto a primary point of the 360-degree compass.

The Maunganui Bluff overland complex of purpose-placed obelisk, mound, sighting-pit or cut benchmark features was an ancient school of learning, where initiates clearly learned surveying, navigation and astronomy.

The author, over 20-years ago, sitting between component markers of the Waitapu standing stone circle. To the left is the southern, tumbled-sideways, hubstone and to the right is one of the giant, recumbent, shark's fin shaped stones that once stood upright. Behind, towards the sea horizon, are many more component boulders hidden by the high grass. The panoramic views from this standing stone site are magnificent.

Here are examples of outlier boulders that stood a coded distance and angle away from one or the other of the two hubstones. Each position provided a number, based either on length away or angle around from north and these numbers generated related to navigation and the equatorial size of the earth, cyclic astronomy durations, the lunisolar calendar or PI & PHI ratios, etc. These standing stone sites around the world, were libraries of scientific principles, encoded by stone positions, that retained their information forever, as long as the stone positions remained intact. Any stone site like this can be easily deciphered as long as one knows the measurement standard used, as well as the 360-degree compass system.

The northern hubstone of the dual hubstone site. This sits due north (0-360-degrees) from the southern hubstone.

The northern hubstone, once again, sitting a measured distance due north of the southern hubstone. The site, and all of its component positions, was surveyed by the author.

Around the site one occasionally encounters these double stone arrangements of approximately the same length and width, with a gap between. They indicated a sighting direction through the gap onto a target.

As can be seen from this picture, there is a horizontal, hand hewn terrace high on the cliff face and behind the terrace it's an almost sheer drop down to the water's edge lapping the base of the cliff.

Lying on one's belly and peering over the back of the level terrace is not for the faint hearted or anyone scared of heights and precipices. In this picture seals can be seen frolicking in the ocean at the base of the sea cliff.

The ancient surveyors would have dropped a rope down on a slight diagonal to the high tide mark, made an angle adjustment to calculate vertical height from sea level, then transferred that reading to secondary stations. By this means they could calculate the height above sea level of surrounding mountains.

The rear side of the hand-hewn terrace is seen here. Across the valley on a flat plateau is the very impressive standing stone circle, with the many component boulders tipped over and lying recumbent in the long grass. Above the former standing stone observatory the gradient rises diagonally to a high plateau and on this slope there is a line of carefully placed obelisk markers that relate specifically, in a surveying sense, to the level terrace on the cliff face seen in the foreground of this picture.

The obelisk line works in the following manner: One sets up a theodolite by an obelisk low on the slope above the observatory plateau and ascertains that they are on a perfect level with the benchmark cleft, level terrace across the valley. One then moves to obelisks at higher levels in the line and sees the sea horizon begin to rise accordingly. At the final, most elevated obelisk position the sea horizon perfectly meets the hewn terrace on the cliff across the valley.

One of the anciently purpose-placed obelisks for working out elevations, above sea level, of hill or mountain targets standing away from Maunganui Bluff and the Waitapu Valley of Northland New Zealand.

In this picture the benchmark terrace is level with the obelisk across the valley, as verified by use of a surveyor's theodolite.

In this picture the obelisk position sits at a level wherein the sea horizon conjuncts with the benchmark cleft cut into the sea cliff.

This was formerly a small standing stone circle on a gently sloping hillside. Many years ago, the farmer, Mr Downey, pushed the outer component boulders to the centre hubstone, a large hefty obelisk. The smaller boulders would once have resided at specific distances and angles away from the hubstone. This is a solar observatory for getting a fix onto the exact day of the summer solstice.

From the hubstone position in the valley one looks at the purpose-built tor-mound on Maunganui Bluff range and witnesses the summer solstice sun’s “first-glint” occurring at the northern base of the mound. However, one can see the same occurrence again when moving swiftly further down the hillside to a second cairn heap.

This is a lower solar observatory that also marks the summer solstice sunrise. By rushing to this position after seeing the sunrise from the hubstone up the hill, one can see the whole rise spectacle for a second time.

From the lower solar observatory site, the summer solstice sun is seen to rise from the southern edge of the tor mound and climb the mound to launch itself into the sky. This well-used modus operandi of having the sun climb up the edge of a hill or mountain at the time of the solstices or equinoxes was incorporated into many purpose-built sites throughout ancient New Zealand.

This huge, heavy obelisk represents the observation position for witnessing the equinox sunset onto the very prominent geological feature of Maunganui Bluff mountain.

A very conspicuous notch formed by flat land and the diagonal slope, below Maunganui Mountain’s summit, gives an exact fix on the equinoctial sunset from the purpose placed obelisk on a low hill crown to the east. The same obelisk gave an accurate fix on the equinoctial sunrise occurring atop the Tutamoe Mountain range.

This giant obelisk is the main component of a stone row of purpose-placed, large obelisks that have all been pushed over to lie in the same direction. They relate to a summer solstice sunset fix onto the high, steep seaward hill seen in the background.

The impressive obelisk line, with all of its former standing components now lying recumbent.

This giant, fallen and broken obelisk sits in a farm field within the Waitapu Valley. It was the observer’s position for witnessing the winter solstice sunrise, occurring on the northern end of the high Tutamoe Range and Marlborough Forest.

Large scale, overland mapping alignments extended from the Waitapu Valley to prominent mountain landmarks within distant view and the evidence shows that triangulation onto the self-same target, from several trigs, was occurring. Using triangulation mathematics, the ancient surveyors were calculating distances and angles to targets and doing accurate land-mapping.

The mountain in the distance, situated inland from the sea coastline near Broadwood, can only be seen from two vantage points some distance apart within the Waitapu Valley. This is due to considerable high ground throughout the valley obscuring the view north. This photo was taken from the benchmark cleft above the coastal cliffs where the observer’s view can skim past high terrain to get a wide panoramic view of the northern mountains.

The laboriously hewn, level cleft can be seen on the declining face of the cliff. Apart from providing a fixed elevation above sea level, it also afforded a rarely available view to the mountains far to the north.

At a distance of 2.32-miles away, NW across the Waitapu valley from the cleft in the cliff is an ancient, purpose-built mound of heaped up rocks and soil. It is surrounded by cairn markers and sighting pits that orientate onto targets to the north and east.

From this vantage point the self-same mountain range comes into view once again. The chopped-out part of the mound to the right is where a roading contractor bulldozed through many years ago when building Hood Road. To the driver’s credit, upon realising that the hump was a purpose-built, man-made structure, the road was moved 175-feet south, thus saving a dynamic ancient archaeological site.

By consequence, our mainstream archaeologists are in denial that such mounds exist and, under their watch, the entire structure would have been eradicated, just like an important nearby carved hilltop site was signed off for destruction and turned into a quarry.

The same seawards mountain (Maungataniwha Range near Broadwood) and the rest of the northern range can be seen anew from the purpose-built, surveying mound on the northern rim of the Waitapu Valley.

The distance and angle looking NW from the sea-cliff cleft to this mound obviously represented a surveyor’s baseline of known length. By taking angle shots from each end of the baseline, the distance to the northern mountain could be calculated with precision. It’s important to realise that the ancient Sumerians were doing accurate trigonometric calculations over 5000-years ago.

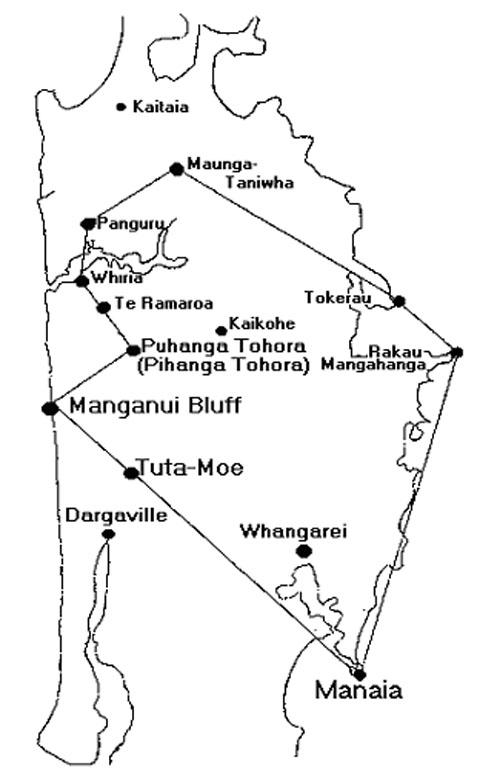
The Ngapuhi iwi (tribe) have preserved evidence of this ancient overland-mapping circuit, component parts of which included Maunganui Bluff and Tutamoe Mountain, in a song passed down by oral tradition:

TE WHARE O NGA-PUHI
He mea hanga
Ko papa-tuanuku te papa-rahi
Ko nga maunga nga poupou
Ko te rangi e titiro iho neu te tuanui
PUHANGA TOHORO titiro ki TE RAMAROA (PIHANGA TOHORA)
TE RAMAROA titiro ki WHIRIA
Ki te paiaka o te riri, ki te kawa o RAHIRI
WHIRIA titiro ki PANGARU, ki PAPATA
Ki te rakau tu papata i tu ki te Taihauru
PANGARU PAPATA titiro ki MAUNGA-TANIWHA
MAUNGA-TANIWHA titiro ki TOKERAU
TOKERAU titiro ki RAKAU-MANGAMANGA
RAKAU-MANGAMANGA titiro ki MANAIA
MANAIA titiro ki TUTU-MOE
TUTU-MOE titiro ki MANGANUI
MANGANUI titiro ki PUHANGA-TOHORA
Ko te whare ia tenei o NGA-PUHI
(from Eru Pou, Kaikohe...recorded by Joan Leaf)

THE HOUSE OF NGA-PUHI
This is how it is made:
The earth is the floor
The mountains the supports
The sky we see above is the roof
From PUHANGA TOHORA look toward TE RAMAROA (PIHANGA TOHORA)
From TE RAMAROA look toward WHIRIA
The seat of our war-like prowess
The ancestral line of RAHIRI
From WHIRIA look toward PANGARU - to PAPATA
To the thickly growing trees which extend to
the western sea
From PANGARU and PAPATA toward MAUNGA-TANIWHA
From MAUNGA-TANIWHA look toward TOKERAU (Bay of Islands)
From TOKERAU to RAKAU-MANGAMANGA (Cape Brett)
From RAKAU-MANGAMANGA to MANAIA (Whangarei Head)
From MANAIA to TUTU-MOE
From TUTU-MOE to MANGANUI BLUFF
From MANGANUI look toward PUHANGA TOHORA
This is the house of NGA-PUHI

On the summit crown of Maunganui Bluff Mountain, a series of cairn mound humps are distributed around the crest. Each of these represent directional markers out to a target around the horizon from the observer’s position at the centre of the crown.

From the top of Tutamoe Mountain (seen from Maunganui Bluff) there is a clear view to Manaia Mountain on the eastern coastline, then up the coast to Rakau Mahanga, etc. This ancient song speaks of mountains that look at each other and is clearly indicating a well-surveyed mapping alignment, passed down in song by oral tradition transmission.